Likformighet
Fick denna uppgift av min lärare, men har fastnat och kommer ingen vart.
Uppgiften lyder:
”Visa att radien är 4,5 cm om du vet att sträckan AB =12cm och CE=9cm.”
Jag fick dessutom en ledtråd av min lärare som menade att man ska dra en sträcka mellan DC, men längre kommer jag inte.
Jag skulle därför uppskatta någon form av hjälp eller ytterligare ledtråd väldigt mycket!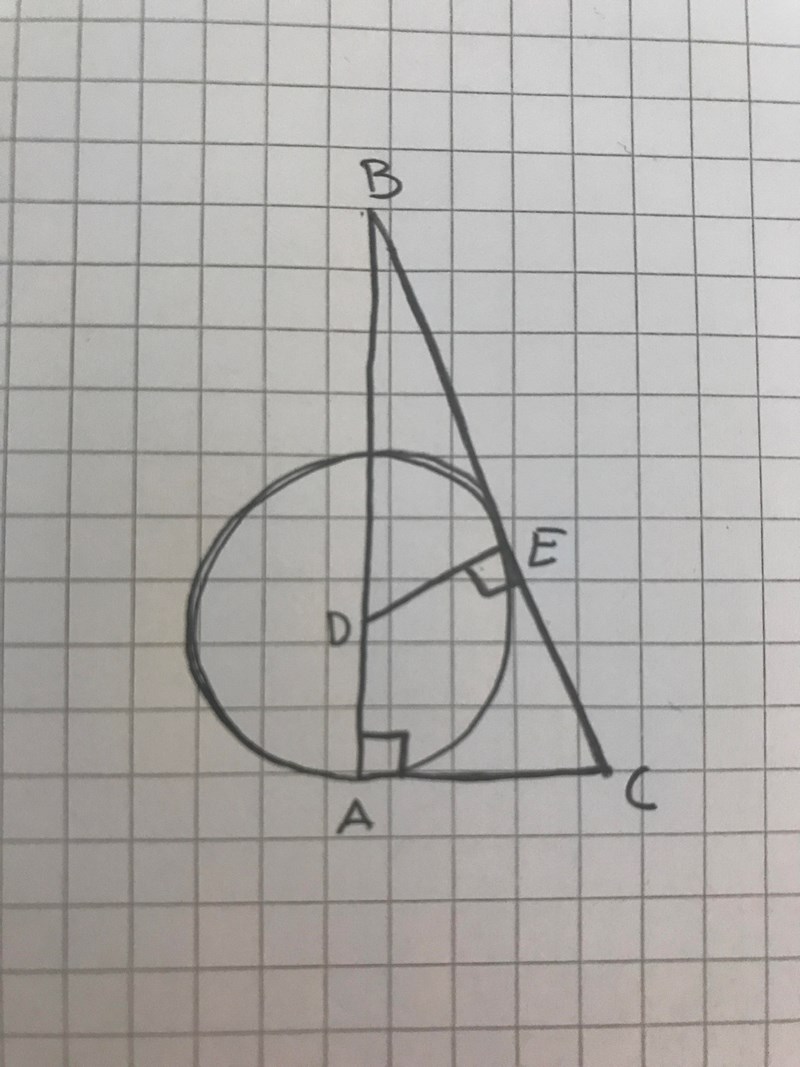
Trianglarna DEC och DAC är kongruenta, så sträckan AC är?
Det kan bli lite lättare om du ritar den skalenligt. Men dra linjen din lärare tipsade om till att börja med och försök lista ut vilka som är lika långa som varandra.
dioid skrev:Trianglarna DEC och DAC är kongruenta, så sträckan AC är?
AC blir då 9cm precis som CE, men jag förstår fortfarande inte hur jag ska få ut radien
Nu när du vet AC och AB så kan du räkna ut BC.
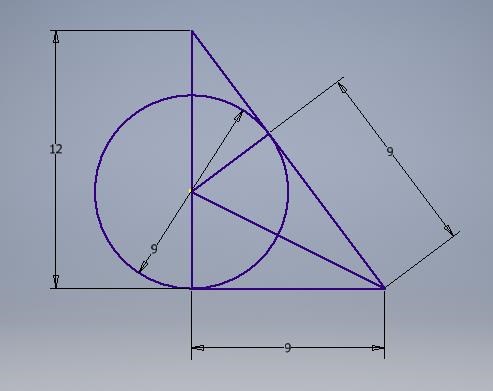
*Spoliers*
1. Pythagoras sats ger: BC=15
2. BE=BC-CE=15-9=6
3. Pythagoras sats igen. x=radien
BD=((x^2)+6^2)^0,5
där BD=AB-x=12-x
4. Renskriver ekv. och lös ut x.
12-x=((x^2)+6^2)^0,5
(12-x)^2=(x^2)+6^2)
144-24x+x^2=36+x^2
144-24x=36
108=24x
x=108/24=4,5 (cm)
vsv.
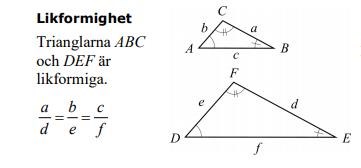
Alltså: Denna formel går inte att använda jättemycket pga tri-ABC är ej kongruent med tri-CDE eller tri-ACD.
(eftersom att DE=AC(CE/AB)=(81/12)=6,75 (cm) )
Med viss reservation för slarvfel : s
Likformighet kan användas för en lite kortare slutkläm på lösningen. BED är likformig med BAC så DE är hälften av AC eftersom BE är häften av AB.

