Limt
Jag vet att när limt f(x) = 0/0 eller inf/inf när x går mot a ska använda lobital roll och derivera både täljare och närmare sen löser det. Men jag försöker med 2 funktioner
[Xsin(x])/[(x+sin(x)]^2 x går mot +inf -inf. Och 0
[(1+x)^(1/2)]-[2x]^(1/2)]/[x^2- x] när x går mot 1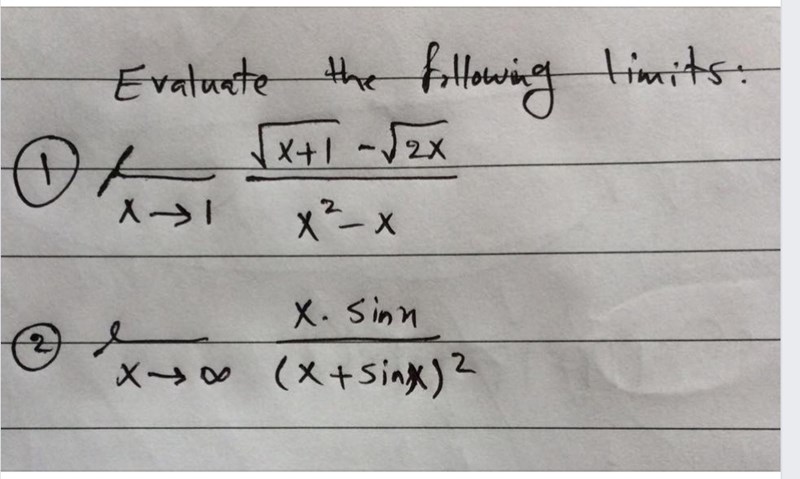
Vad det gäller första uppgiften: Börja med att undersöka om L'Hospitals regel kan användas här. Är funktionerna kontinuerliga och deriverbara då x = 1? Jo, men det verkar gå bra.
Insättning av x = 1 i funktionerna ger att och . Vad blir då gränsvärdet?
Angående den andra frågan: Här ska inte L'Hospital användas. Dividera alla termer med den dominerande faktorn, och förenkla.
Är jag testar med inf blir det. [Inf * ?)] /[(inf+?)^2] det betyder limt saknas
Hur har du fått det? :) Börja med att identifiera den dominerande faktorn. Vilken är det? Vad får du om du dividerar alla termer med denna?


