limt
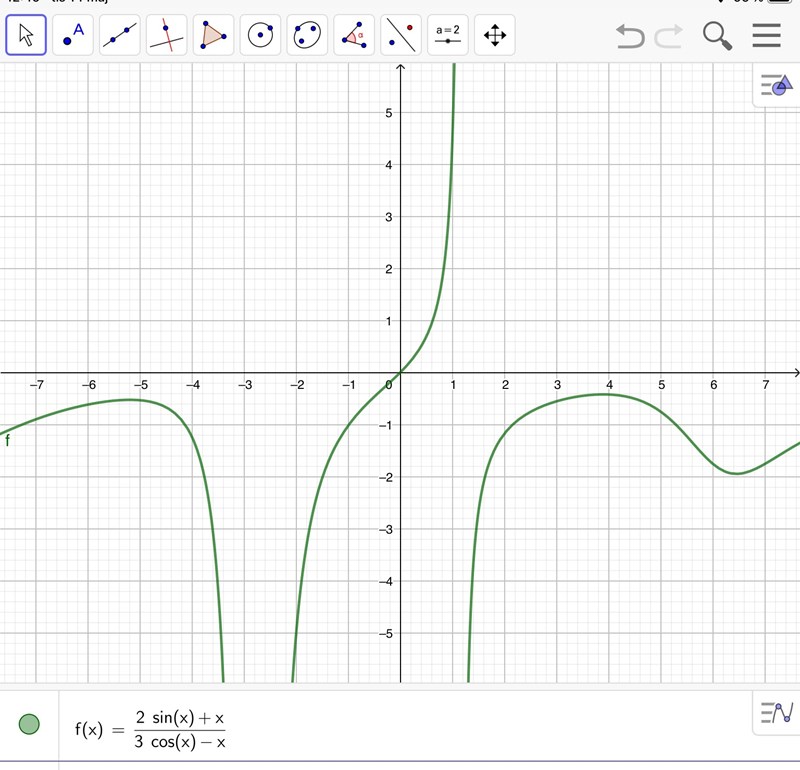
Undrar om det är rätt, men när jag ritat, det blir inte - 1
Jag tror du har tänkt rätt, men det går inte riktigt förlja din uträkning. Likheten i första ekvationen är något du vill bevisa, eller hur? Andra raden är en en omskrivning av första raden? Tredje och fjärde raderna är hjälpberäkningar, medan femte raden är en omskrivning av ursprungsuttrycket igen, och den här gången har du beräknat gränsvärdet, och därmed visat att dina första två ekvationer är uppfyllda?
Jag hade istället skrivit det som
Att det inte syns i figuren betyder att du inte ritat x-axeln tillräckligt långt
Tack för svaret, en andra tanke som jag tänkt är att när x går mot inf är det så snabbt och stort om man jämför med sin(x)och cos (x) ,samtid lim of de två trigonometriska är begränsad mellan [-1,1] kan mot ta bort from lösningen.
Om Jaf görpå provet blir det godkänt
Det är ett bra sätt att resonera på, men vill du bevisa det ordentligt så är det så som du gjorde i din första lösning som gäller. Men är det ett matte 4 prov kan jag tänka mig att ditt andra resonemang duger, jag är osäker på hur rigorös man måste vara där.

