Lineär algebra
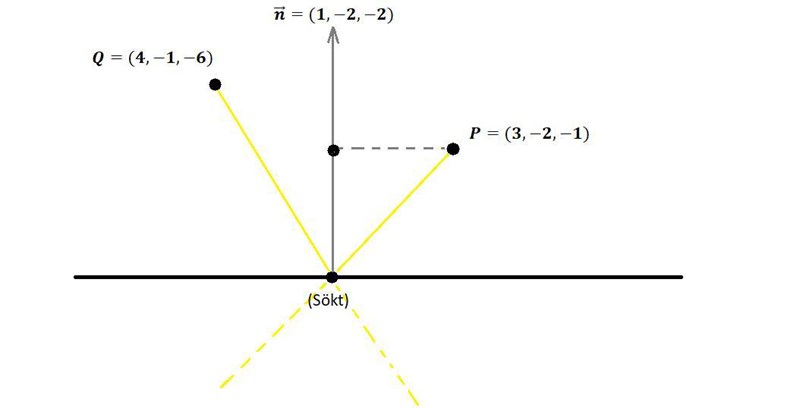
En ljusstråle som utgår från punkten reflekteras mot planet
Den reflekterande strålen går genom punkten .
I vilken punkt träffar ljusstrålen planet?
(projektionsformeln får inte användas)
Hur ska jag tänka?
Jag har tänkt följande:
- Att försöka hitta linjerna för "strålarna"
- hitta linjen för projektionen på normalen
- beräknat linjen som går genom de två kända punkterna, vilket har medfört:
(här har jag dock fått slut på ideer)
Punkten i planet är
(2y + 2z,y,z)
Vektorn därifrån till (3,-2,-1) har samma (cosinus för) vinkel till normalen som därifrån till (4,-1,-6).
Det borde gå att härja ut y och z från detta.
Edit: Läste inte frågan ordentligt, det här räknas förmodligen som en projektion i första steget eftersom
Låt
Nu ställer vi oss i P och går t steg längs tills vi hamnar i planet.
Vår sökta punkt blir
Jag väljer att bygga min tankegång utifrån ortsvektorer. Minns att O:(0,0,0) ligger i planet.
Känner mig bekväm med detta sätt att resonera. Beteckningar enligt figur.
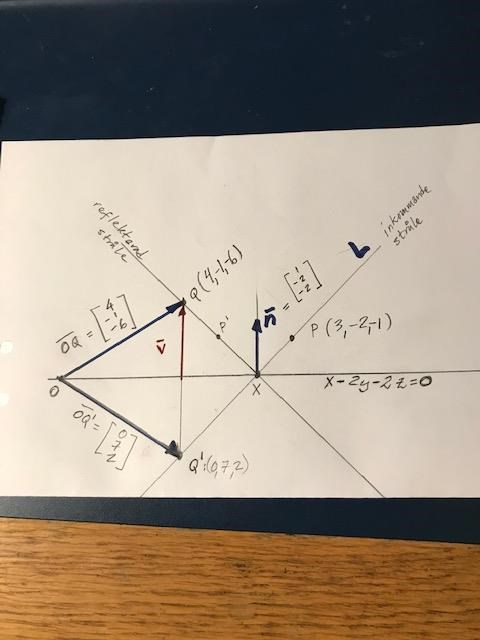
Det innebär att . Vektor , där enhetsnormalvektorn
Spegelpunkten bestäms genom , dvs
, varav .
Inkommande linje L har riktningsvektor .
Linjen L parametriseras: .
Sökta punkten X fås slutligen genom att sätta in parametriseringen i planets ekvation:
, varav , och .




