Linearisera rörelseekvationerna och hitta vinkelhastigheterna
Hej!
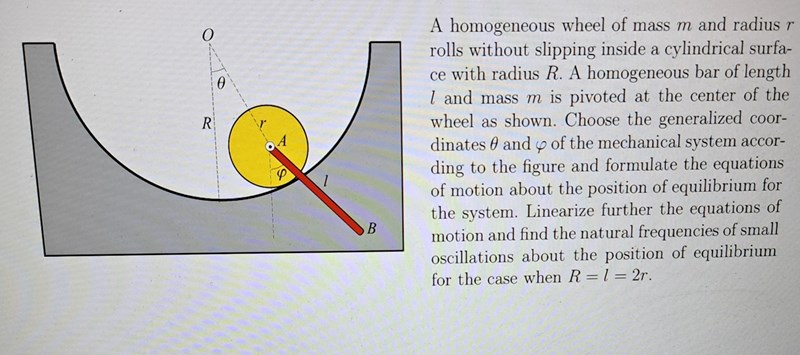
Jag vill införa theta och phi som generaliserade koordinater för att teckna L=T-V osv. Men är osäker på om jag tänker rätt här. En annan sak jag undrar över är hur jag ska tänka med T1 som kommer från A då A består av x_A och y_A ?
xA=(R-r)sintheta
yA=-(R-r)costheta
xG=x_A+l/2sinphi
yG=y_A-l/2cosphi
Hastigheten är en vektor men i kvadrat är den en skalär. Alltså kommer du få ett värde om du deriverar dina lägen och sedan kvadrerar.
Använd gärna formler som du redan kan direkt map valda koordinater. Exempelvis är . Stångens hastighet kommer ges av hastigheten av A relativt O + hastigheten för stångens masscentrum relativt A. Cosinussatsen lämpas bra för den vektoradditionen.
MrPotatohead skrev:Hastigheten är en vektor men i kvadrat är den en skalär. Alltså kommer du få ett värde om du deriverar dina lägen och sedan kvadrerar.
Använd gärna formler som du redan kan direkt map valda koordinater. Exempelvis är . Stångens hastighet kommer ges av hastigheten av A relativt O + hastigheten för stångens masscentrum relativt A. Cosinussatsen lämpas bra för den vektoradditionen.
Ja jag snackade med Ai i väntan på PA:s hjälp. Jag har nu en lagrange funktion som skall deriveras. Kör jag fast så säger jag till eller om svaren jag fått fram inte stämmer med facits svar.


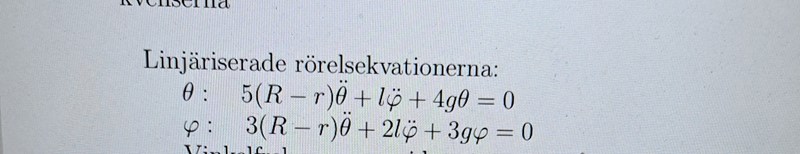
Jag får inte riktigt samma term som facit när det gäller theta och phi. Jag saknar en phiprickprick samt en gtheta som jag inte vet var de fått det ifrån.


Jag vet inte varför jag saknar 2gtheta faktor.


