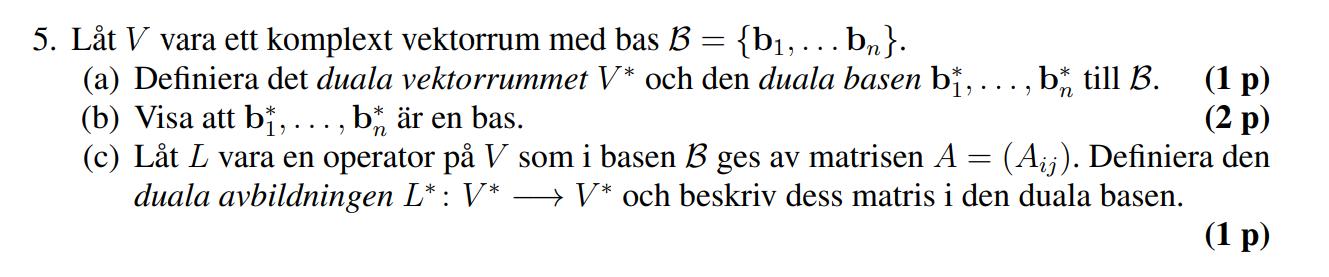Linjär algbra: Betydelsen av dualbas

Du kan förståss välja vilken bas du vill i dualrummet. Men det verkar som att du ska undvika att kalla den för dualbas om den inte är biortogonal mot en bas i det ursprungliga rummet. Man får väl nöja sig med att säga att det är en bas i det duala rummet, varken mer eller mindre.

https://en.m.wikipedia.org/wiki/Dual_basis

Begreppet "dualbas" är inte samma sak som "bas för ett dualrum", utan är precis som du är inne på ett mycket mer specifikt begrepp. Dessutom makear ordet "dualbas" inte ens riktigt sense i isolation, utan jag tycker att det alltid bör följas (måhända implicit ibland) av ett "till" (eng. of), eftersom själva definitionen bygger på en relation till en redan vald bas för vektorrummet man jobbar med.

Mer precist så brukar man ju introducera begreppet ungefär så här:

Definition. Låt $V$ vara ett vektorrum över en kropp $k$, och låt $\mathcal{B}=\{\mathbf{e}_i\}_{i\in I}$ vara en bas för $V$. Dualmängden till basen $\mathcal{B}$ är då definierad som mängden $\mathcal{B}^*=\{\varphi_i\}_{i\in I}$ där funktionalerna $\varphi_i\colon V\to k$ är definierade av $\varphi_i(\sum_{i\in I} \alpha_i\mathbf{e}_i)=\alpha_i$.

Och sedan visar man att detta gäller:

Sats. Låt $V$ vara ett vektorrum över $k$, och låt $\mathcal{B}$ vara en bas. Då gäller följande:

(i) Dualmängden $\mathcal{B}^*$ en linjärt oberoende delmängd av dualrummet $V^*$.

(ii) Om $V$ är ett ändligt-dimensionellt vektorrum, så kommer $\mathcal{B}^*$ även att spänna upp $V^*$ (dvs. det kommer att vara en bas för $V^*$). 

I det ändligt-dimensionella fallet, där (ii) gäller, så kallar man $\mathcal{B}^*$ för dualbasen till basen $\mathcal{B}$.

Anledningen jag frågade detta var för att jag pluggade på en gammal tenta och denna fråga kom upp:

men den är ju meningslös i alla fall med min uppfattning av begreppet. Jag tycker att läraren borde använt $e_i^*$ för att betona att basen är kanonisk på nåt sätt. Min första instinkt var "va? jag vet inte ens vad $b_i^*$ är för nåt" sedan "jo jag vet vad det är för nåt, det är en bas för att you just said so".

Och ja, på b) frågan bevisade jag att B* är lin.ob. och spänner V*.