Linjär Algebra - Bestäm alla högerinverser av 4x3 matris
Hej. Detta är en gammal tentafråga. 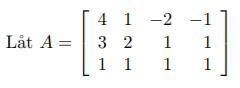
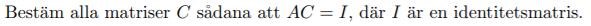 För att räkna ut inversen av matrisen konstruerar jag den utökade matrisen [ A I3 ] och radreducerar den till trappstegsform.
För att räkna ut inversen av matrisen konstruerar jag den utökade matrisen [ A I3 ] och radreducerar den till trappstegsform.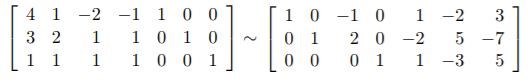
Men vad är det man ska göra sen? Det har ju något med vektorparametrisk form att göra, men det är lite svårare än vanligt här känns det som. Btw, jag vet att det säkert finns 1000 andra sätt att lösa den här uppgiften på...
Det första du ska göra är att kontrollera rangen för matris A. Då frågan är ställd som den är kan antas att den har rang 3 men det kan ändå vara bra att dubbelkolla. Sedan är det enklast att hitta högerinversen för A genom QR-faktorisering.
https://sv.wikipedia.org/wiki/QR-faktorisering
Det du försöker göra är bara giltigt för kvadratiska matriser. Förövrigt är det inte trappstegsform som söks utan att erhålla identitetsmatrisen på vänstersidan.
Välkommen till Pluggakuten!
Matrisen A har rader och kolonner så den är av typ För att multiplikationen ska vara definierad måste matrisen vara av typ , vilket ger en produkt som är av typ För att produkten ska vara en identitetsmatris (som är kvadratisk) så måste , vilket betyder att den sökta matrisen måste vara av typ
- Om du multiplicerar ekvationen från vänster med transponatet får du
- Om den kvadratiska matrisen (som är av typ ... ) är inverterbar (undersök om den är det!) så fås den sökta matrisen som produkten
Albiki skrev:
- Om den kvadratiska matrisen (som är av typ ... ) är inverterbar (undersök om den är det!) så fås den sökta matrisen som produkten
är inte inverterbar.
Hej! Jag borde nog ha sagt att jag tog urklipp ur FACIT, alltså inte mina anteckningar. Det är exakt den metoden som jag beskrev som används för att lösa uppgiften. Som jag skrev så vet jag att det finns andra sätt att lösa uppgiften på men i facit så används metoden som jag beskrev, så det är antagligen den rätta metoden för just det här problemet. I vilket fall, här är lösningen, från FACIT i sin helhet: 

Det verkar tydligt att denna lösning är ganska okänd så det vore kul om någon som verkligen förstår denna lösningen kan förklara hur man ska göra.
josefjson skrev:Hej! Jag borde nog ha sagt att jag tog urklipp ur FACIT, alltså inte mina anteckningar. Det är exakt den metoden som jag beskrev som används för att lösa uppgiften. Som jag skrev så vet jag att det finns andra sätt att lösa uppgiften på men i facit så används metoden som jag beskrev, så det är antagligen den rätta metoden för just det här problemet. I vilket fall, här är lösningen, från FACIT i sin helhet:
Det verkar tydligt att denna lösning är ganska okänd så det vore kul om någon som verkligen förstår denna lösningen kan förklara hur man ska göra.
Jag har aldrig någonsin sett denna specifika lösningsmetod men det är en form av QR-faktorisering. Jag skulle inte försöka lära mig detaljerna utan bara kopiera tillvägagångssättet om jag var du då detaljerna borde blivit utlärda under normalt kursflöde. Är det något som är oklart i vad som händer och i vilket steg har du frågetecken?


