Linjär algebra: definiera metriktensorn utan en inre produkt
Hej, se:
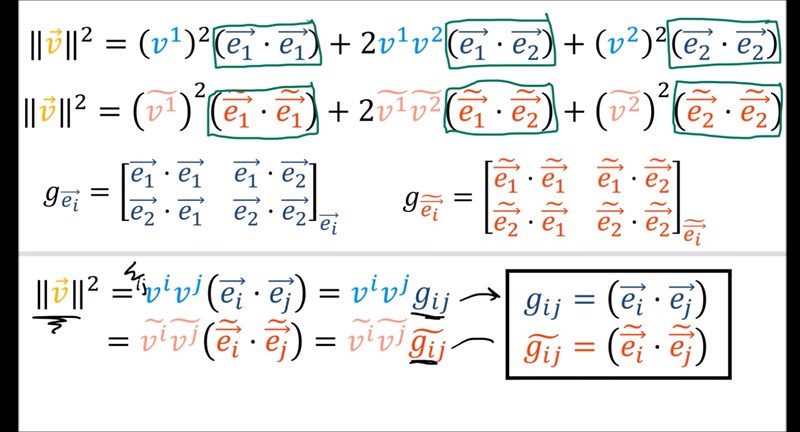
Metriktensorn definieras i videon med något så ogenerellt som skalärprodukten, men visst går det att göra med någon annan inre produkt? Vad händer om vi inte har tillgång till nån inre produkt?
Glöm det, jag har blandat ihop helt...
Hur definieras en skalärprodukt? Hur definieras en tensor? Kan man definiera en skalärprodukt i termer av en tensor?
En del böcker definierar det som följer.
En skalärprodukt är en symmetrisk andra ordningens tensor g som uppfyller att
om g() = 0 för alla , så är = 0, dvs nollvektorn är den enda vektor som är ortogonal mot alla vektorer.
Denna definition är lite generellare än definitionen av inre produkt.
Sedan skriver man g() = •.
En lustig och (lite) mer generell definition är (med beteckningar från din tråd om tensorer)
Öh... ni menar alltså att inre produkten definieras med tensorer och inte tvärtom?
Du kan ju göra det åt vilket håll du önskar.
Om du har en skalärprodukt • så kan du definiera den metriska tensorn g genom
g(x, y) = x•y.
Alternativt, om du har en tensor g som uppfyller axiomen som jag nämnde, definierar vi skalärprodukten • genom
x•y = g(x, y).
Jag tror att Jroths definition gör att vi får en skalärprodukt/metrisk tensor där vår bas e1, ..., en blir en ON-bas.
Om man har en en differentierbar mångfald som saknar metrik är den inre produkten endast möjlig genom parbildning mellan en ko- och kontravariant vektor.
Men om du faktiskt har en metrik kan du som pantenteramera förklarar definiera den inre produkten av två kontravarianta vektorer som den bilinjära formen
Och i linje med hur man slarvar lite med saker säger vi att är en (0,2)-tensor (den metriska tensorn) som gärna vill äta upp två kontravarianta vektorer och spotta ur sig en skalär.
Edit: Och eftersom frågan kanske egentligen var hur man definierar den metriska tensorn så är en god kandidat:
Låt
Där funktionen F som i någon mening mäter längden är tillräckligt många gånger deriverbar i alla argument och oberoende av i vilket koordinatsystem vi använder. Vidare ska
för alla
Beroende på vilka ytterligare villkor vi påför får vi olika geometrier.
Särskilt gäller att om bara av beror av samt har vi en Riemanngeometri (med den metriska tensorn).
Det finns andra villkor och väger att gå, jmfr t.ex. Finsler --> https://en.wikipedia.org/wiki/Finsler_manifold




