Linjär algebra: etymologi "kvot"rum?

Jag tror att det kommer sig av motsvarande begrepp inom gruppteorin, kvotgrupp.

Och kvotgrupp heter det nog för att det typiska första exemplet är att den homomorfism som avbildar  Z på gruppen av heltal modulo n har gruppen av heltal delbara med n som nollrum. Så gruppen av heltal modulo n kan betraktas som kvoten när Z delas med Zn, heltalen delbara med n.

Inte så konstigt att jag inte visste om det isåfall, kan inget om gruppteori. 

Tack!

Kvotkonstruktioner finns överallt i matematiken! Du verkar vara mest bekant med kvotrum i linjär algebra, och som redan har nämnts är kvotgrupper ett centralt koncept i gruppteori. Själv stötte jag på kvoter för första gången i ringteori där man ofta talar om kvotringar, och som topologifantast vill jag slå ett slag för topologiska kvotrum* (även om det kanske är lite off topic här).

Det alla sådana här kvotkonstruktioner har gemensamt är att man utgår från en mängd $X$ (som eventuellt har någon extra spännande struktur) och sedan inför en ekvivalensrelation $\sim$ som gör det möjligt att identifiera element i $X$ med varandra. Detta ger oss en uppdelning (en partition) av $X$ i disjunkta delmängder som vi kallas för ekvivalensklasser, och kvotmängden $X/\sim$ är helt enkelt mängden av alla sådana ekvivalensklasser (en mängd av mängder alltså).

Schematiskt kan vi tänka oss bildandet av den här kvotmängden på följande vis:

Vi har en påse $X$ med saker, inför något slags ekvivalensrelation (t.ex. genom att bestämma att två objekt är ekvivalenta omm de har samma färg) och stoppar sedan alla saker som är ekvivalenta i egna små påsar och lägger dem i en stor påse ("ordning och reda, pengar på fredag!").

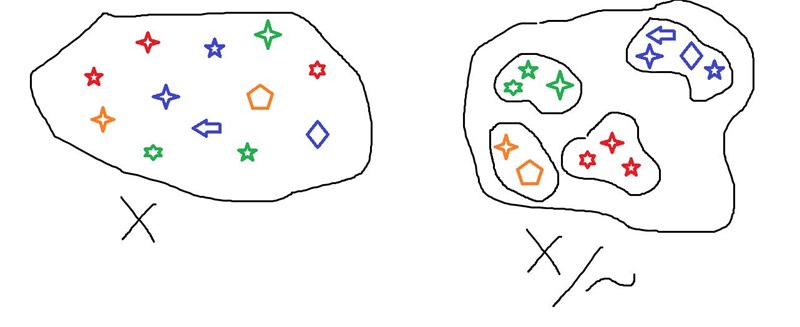Vad har nu detta med division att göra? Ärligt talat kanske inte jättejättemycket, men det finns några vaga kopplingar:

(i) Bilden jag ritade ovan liknar de bilderna man ritar när man introducerar division av positiva heltal på lågstadiet.

(ii) Båda koncepten har någon slags diffus känsla av att man kollapsar en stor mängd till något mindre. Dessutom har $X$ och $\sim$ lite liknande påverkan på slutresultatet som täljare respektive nämnare vid vanlig division:

• Om $X$ blir mindre så kan vi förvänta oss att $X/\sim$ också blir mindre eller i vart fall inte större.
• Om $\sim$ blir mindre (så till vida att vi blir mindre generösa med hur grova identifikationer vi gör) så blir $X/\sim$ större eller i vart fall inte mindre.

Exempel: Om vi i vår bild ovan gör $X$ mindre genom att ta bort alla de orange figurerna så blir det en färre ekvivalensklass i $X/\sim$. Om vi gör $\sim$ mindre (alltså mindre flexibel) genom att kräva att både färgen och antalet hörn överensstämmer så kommer vi få många fler ekvivalensklasser i $X/\sim$.

(iii) För vektorrum uppfyller kvotkonstruktionen en slags "potenslag" som påminner om vanlig division: om $V$ är ett $n$-dimensionellt vektorrum och $W\subseteq V$ är ett $m$-dimensionellt underrum, så kommer $V/W$ [som är samma sak som kvotmängden $V/\sim$ för $v\sim v'$ omm $v-v'\in W$, utrustad med den uppenbara additionsoperationen och skalningsoperationen] att vara $(n-m)$-dimensionell. Lite slarvigt kan vi uttrycka detta som "$\mathbb{R}^n/\mathbb{R}^m=\mathbb{R}^{n-m}$".

(iv) Som redan har nämnts i tråden är ett av de mest prototypiska exemplen på kvotkonstruktioner kvotgruppen (eller om man så vill: kvotringen) $\mathbb{Z}/n\mathbb{Z}$ (alltså heltalen mod $n$) som består av alla restklasser vid division med $n$, och det har ju helt klart en koppling till division, även om notationen kanske ändå inte är så jättenaturlig.

* Ett kul exempel på ett topologiskt kvotrum är det klassiska datorspelet Asteroids (går bl.a. att spela här), där den övre kanten av skärmen är identifierad med den undre kanten, och vänsterkanten är identifierad med den undre kanten, vilket får konsekvensen att spelet utspelar sig i ett rum som är homeomorft med en torus (se exv. den här figuren)!

Finns det alltid en ekvivalensklass som gör att varje element endast är ekvivalent med sig själv respektive alla ekvivalenta med alla?

(fler frågor snart)

Qetsiyah skrev:

Finns det alltid en ekvivalensklass som gör att varje element endast är ekvivalent med sig själv respektive alla ekvivalenta med alla?

Helt rätt! Låt $X$ vara en valfri mängd (med minst två element). Då kan vi alltid hitta på två triviala ekvivalensrelationer:

• Den jätteflexibla ekvivalensrelationen som säger att alla element är ekvivalenta, dvs. $x\sim x'$ för alla $x,x'\in X$.
• Den jättekräsna ekvivalensrelationen (a.k.a. likhetsrelationen) som säger att varje element bara är ekvivalent med sig självt, dvs. $x\sim x'$ omm $x=x'$.

Övning: Beskriv hur $X/\!\sim$ ser ut i båda de här fallen (t.ex. genom att modifiera min fina paint-bild!).

Rent allmänt kan man säga att en viktig del i matematiskt arbete är att hitta ekvivalensrelationer som hittar den perfekta balansen mellan de här två ytterligheterna - som är lagom flexibla respektive kräsna för de situationener man studerar.

Lite kul sätt att beskriva: |X/~|=1 eller |X|!

Då förstår jag vad ekvivalensrelation betyder!

Helt korrekt! ^_^

Från vänster till höger: $X/\!\sim$ för den jätteflexibla respektive den jättekräsna ekvivalensrelationen.

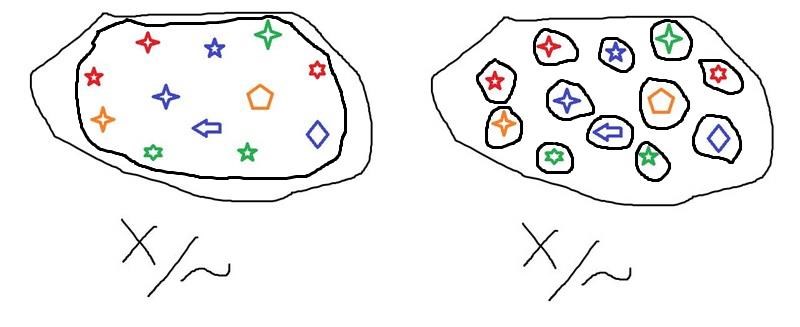
(Men för guds skull: avsluta aldrig en mening med en matematisk symbol och sedan ett utropstecken. Nu ser det nästan ut som att du har räknat antalet bijektioner $X\to X$ ;-))

Åh? Är det så man skriver antalet bijektioner från X till X? Är det någonsin ändligt för en mängd med oändligt mänga element?

Om $X$ är en ändlig mängd så är antalet bijektioner $X\to X$ (dvs. antalet permutationer av mängdens element) lika med $|X|!$. Man brukar skriva mängden av alla sådana "självbijektioner" eller permutationer (eller symmetrier som man ibland också säger) som $\mathrm{Sym}(X)$. Med andra ord är $|\mathrm{Sym}(X)|=|X|!$.

Om $X$ är oändlig så är det enkelt att övertyga sig om att $\mathrm{Sym}(X)$ också är oändlig.

Övning: Visa att $\mathrm{Sym}(\mathbb{N})$ har större kardinalitet än $\mathbb{N}$, och mer precist att $|\mathrm{Sym}(\mathbb{N})|=|\mathbb{R}|$.

Öh... alltså samma kardinalitet som R? Det var inte lite. Låt mig tänka.

edit1: Jag ska hitta en bijektion mellan SymN och R?

edit2: först noterar jag att R har samma kardinalitet som [0,1]

Jag vill bara kommentera lite i efterhand att kvotrum i linjär algebra makear mycket mer sense nu när jag sett det i gruppteori. Det är ju mycket likt vanlig division, eller i all fall den vanliga divisionens andemening.

Oggih dina bilder va också bra men det var bara i en ändlig mängd, jag tror det var svårt för mig att överföra den idén till linalg när jag skapade tråden.