Linjär algebra: normabilitet hos topologiska vektorrum, skillnad mellan T1 och Hausdorffrum

Jag är osäker på vad din fråga är. T1 säger att alla enpunktsmängder är slutna(så alla ändliga mängder slutna) medan Hausdorff säger att alla punkter som inte är lika kan skiljas åt av en öppna mängder. Ett topologiskt rum som är T1 men inte Hausdorff är R med "finite complement topology" dvs där de öppna mängderna är tomma mängden samt mängder med ändligt komplement. Varje par av öppna icke-tomma mängder i denna topolgi kommer skära varandra.

Öh... Jag kan inte förstå det du skriver.

A topological space (X, T) is called a T1 space if, for every two distinct points x, y in X, there is an open neighbourhood U_x  of x that does not contain y. In a topological vector space, this is equivalent to requiring that, for every x neq 0, there is an open neighbourhood of the origin not containing x.

Note that being T1 is weaker than being a Hausdorff space, in which every two distinct points x,y in X admit open neighbourhoods U_x of x and U_y of y with U_{x} snitt U_{y}=tomma mängden since normed and normable spaces are always Hausdorff, it is a “surprise” that the theorem only requires T1.

Jag förstår från wikitexten vad T1 och Hausdorff betyder, men för mig låter de ekvivalenta. Den enda skillnaden jag kan se är att T1 inte verkar kräva att även den andra punkten, y, ska ha en öppen omgivning som inte innehåller x (som i topologisammanhang kanske kallas reflexivitet?), men Hausdorff kräver det.

Men hur kan det ens hända? Att x har en öppen omgivning som inte innehåller y, men inte tvärtom?

Du verkar tolka det rätt. Det kan hända som jag skrev ovanför om man låter de öppna mängderna vara de mängder som har ändligt komplement. Om vi då har en oändlig mängd som vår grundmängd X och två icke-tomma öppna mängder i X så måste de skära varandra, eftersom vardera mängd innehåller alla utom ändligt många element ur X.

Edit: Jag läste ditt inlägg för snabbt, du tolkar det inte helt rätt. Om vi fixerar 2 godtyckliga skilda punkter x och y så säger T1: Det finns en öppen omgivning kring x som inte innehåller y. Och det finns en öppen omgivning kring y som inte innehåller x. Haussdorff är starkare och säger: Det finns en öppen omgivning till x och en öppen omgivning till y som är sådana att deras snitt är tomt. Här kollar man alltså på två omgivningar samtidigt och man får då problem om alla ens öppna omgivningar är "för stora" som i exemplet jag gav ovan.

parveln skrev:

Edit: Jag läste ditt inlägg för snabbt, du tolkar det inte helt rätt. Om vi fixerar 2 godtyckliga skilda punkter x och y så säger T1: Det finns en öppen omgivning kring x som inte innehåller y. Och det finns en öppen omgivning kring y som inte innehåller x. Haussdorff är starkare och säger: Det finns en öppen omgivning till x och en öppen omgivning till y som är sådana att deras snitt är tomt. Här kollar man alltså på två omgivningar samtidigt och man får då problem om alla ens öppna omgivningar är "för stora" som i exemplet jag gav ovan.

Yes, yes, yes. Utifrån min geometriska intuition om Rn låter det väldigt konstigt att ha ett topologiskt rum som är T1 men inte Hausdorff.

Kan du förklara de två exemplerna här: https://topospaces.subwiki.org/wiki/T1_not_implies_Hausdorff

Ett roligare och mer visuellt exempel på ett T1-rum som inte är Hausdorff är $\mathbb{R}^n$ med den så kallade Zariski-topologin, som man använder inom algebraisk geometri.

Den definieras helt enkelt genom att man säger att de slutna delmängderna är precis lösningsmängderna till system av (ändligt många) polynomekvationer i $n$ variabler. Exempelvis är parablen

   $\{(x,y)\in\mathbb{R}^2:y-x^2=0\}$

eller enhetscirkeln

   $\{(x,y)\in\mathbb{R}^2:x^2+y^2-1=0\}$

typsika exempel på Zariski-slutna delmängder i $\mathbb{R}^2$. Men även enpunktmängder är slutna, till exmpel:

   $\{(x,y)\in\mathbb{R}^2:x=1,y=0\}\,.$

Den tomma mängden är också Zariski-sluten, eftersom den kan beskrivas som lösningsmängden till en omöjlig polynomekvation:

   $\varnothing=\{(x,y)\in\mathbb{R}^2:1=0\}$

och hela $\mathbb{R}^2$ är också Zariski-sluten, eftersom det är lösningsmängden till den mest triviala ekvationen av de alla:

   $\mathbb{R}^2=\{(x,y)\in\mathbb{R}^2:0=0\}$.

Illustration över dessa samt ytterligare några andra exempel:

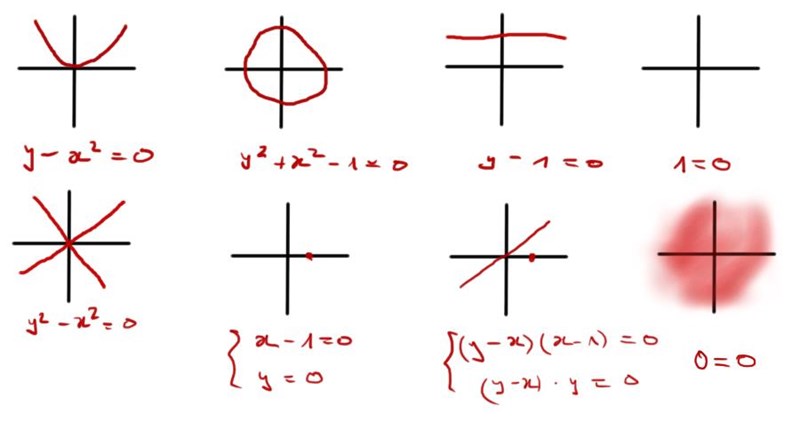
De Zariski-öppna mängderna defineras som komplementen av de Zariski-slutna mängderna. Det är alltså mängder som består av hela $\mathbb{R}^n$ minus ett ändligt antal punkter, polynomiella kurvor, ytor etc. Ett typiskt exempel skulle kunna visualiseras så här:

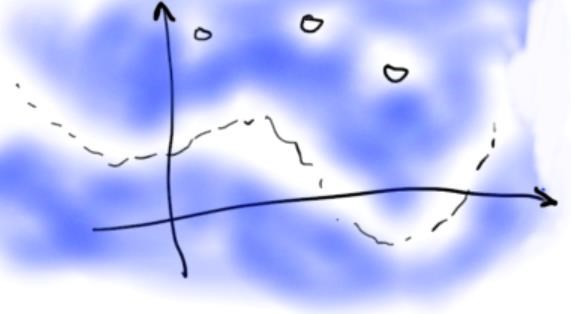
Speciellt innebär detta att alla Zariski-öppna mängder i $\mathbb{R}^n$ (förutom $\varnothing$) är jättestora, eftersom de bitar som skärs bort av lösningsmängden till ett system av polynomekvationer kommer vara väldigt små (ha måttet noll, för att uttrycka sig måtteoretiskt). Speciellt kommer två Zariski-öppna mängder skära varandra nästan överallt, så Zariski-topologin är inte ens nära att vara Hausdorff! Om du har två punkter $p\neq q$ i $\mathbb{R}^n$, så är det omöjligt att välja Zariski-öppna omgivningar $U$ och $V$ runt $p$ respektive $q$, utan att $U$ och $V$ överlappar.

Men Zariski-topologin är T1. Om vi till exempel har två punkter $(a,b)\neq (c,d)$ i $\mathbb{R}^2$, så kan vi notera att enpunktsmängden $\{(c,d)\}$ är Zariski-sluten (det är lösningsmängden till ekvationssytemet $x-c=0,y-d=0$). Därmed är komplemenetet $U=\mathbb{R}^2\setminus\{(c,d)\}$ en Zariski-öppen omgivning av $(a,b)$ som inte innehåller $(c,d)$. På motsvarande sätt är ${\mathrm{ℝ}}^2\setminus \left\{(a,b)\right\}$ en Zariski-öpppen omgivning av $(c,d)$ som inte innehåller $(a,b)$. Precis vad vi behöver visa enligt definitionen!

Slutsats: Det finns T1-rum som inte är Hausdroff, dvs. Hausdorff-kriteriet är strikt starkare än T1-kriteriet.

En naturlig fråga är varför bryr man sig om den här konstiga Zariski-topologin... Det får du nästan läsa en kurs i algebraisk geometri för att få ett riktigt bra svar på, men två saker man ändå kan säga är följande:

• Den går att definiera en Zarkiski-topologi på $\mathbb{F}^n$ för vilken kropp $\mathbb{F}$ som helst! För de flesta kroppar (till exempel ändliga kroppar och deras algebraiska höljen) finns det inget naturligt avståndsbegrepp som kan användas för att definiera öppna bollar. System av polynomekvationer däremot är att rent algebraiskt koncept som makear sense i alla kroppar. Zariski-topologin blir därför en viktig grund om man vill börja tänka geometriskt i sammanhang som vid första anblicken är rent algebraiska, till exempel talteori (där beviset av Fermats stora sats är en av de mest kända framgångssagorna för modern algebraisk geometri).
• Om kroppen vi jobbar över är algebraiskt sluten (till exempel $\mathbb{F}=\mathbb{C}$) så kommer Zariski-topologin på $\mathbb{F}^n$ att vara intimt sammankopplad med den algebraiska strukturen hos ringen $\mathbb{F}[x_1,\ldots,x_n]$ av alla polynom över $\mathbb{F}$ i $n$ stycken variabler. Det precisa påståendet kallas för Hilberts Nullstellensatz, och handlar om polynomringens så kallade radikala ideal (ett av många exempel på hur algebraisk terminologi låter jättepolitiskt!).

Jag ska smälta det här... men medans så har jag följdfrågor om själva frågan och en fundering.

Handlar det här om linjär algebra längre?

Är kolmorgorovs klassificering "totalt ordnad"? (Hehe) alltså att ett rum är av en typ så uppfyller den alla understående? Jag såg den listan på wikipedia.

Det känns som att Zarskislutna mängder i Rn beter sig mycket som linjära underrum till Rn, att den måste vara oändlig åt nåt håll. Det får inte vara en liten "plätt" eller ett linjesegment. Jag vet att cirkeln är lite udda för den är begränsad, men den är i alla fall inte ett linjesegment. Jag vet inte hur jag ska beskriva det.

Qetsiyah skrev:

Handlar det här om linjär algebra längre?

Nja, det här har nog inte så mycket med linjär algebra att göra. Speciellt är $\mathbb{R}^n$ med Zariski-topologin inget topologiskt vektorrum (additionen misslyckas med att vara kontinuerlig).

Jag uppfattade frågan som att du rent allmänt undrade om ett topologiskt rum kan vara T1 utan att vara Hausdroff, och då var Zariski-topologin ett kul exempel ^_^

Någon som är mer hemma på analys än mig kan kanske hitta på ett exempel på ett topologiskt vektorrum som är T1 men inte Hausdroff? Vore intressant att se...

Är kolmorgorovs klassificering "totalt ordnad"? (Hehe) alltså att ett rum är av en typ så uppfyller den alla understående? Jag såg den listan på wikipedia.

Ja! Så vitt jag kommer ihåg ska det gälla att $T_i\implies T_j$ om $i>j$ och $i,j\in\{0,1,2,2\tfrac{1}{2},3,3\tfrac{1}{2},4,5,6\}$. Är nog en ganska enkel övning att kontrollera detta om du går in och läser Wikipedia-artiklarna om alla kriterierna! ^_^

Det känns som att Zarskislutna mängder i Rn beter sig mycket som linjära underrum till Rn, att den måste vara oändlig åt nåt håll. Det får inte vara en liten "plätt" eller ett linjesegment. Jag vet att cirkeln är lite udda för den är begränsad, men den är i alla fall inte ett linjesegment. Jag vet inte hur jag ska beskriva det.

Ibland känns det som att du har läst i förväg ;) För du är absolut något på spåret här!

En bra intuition är att Zariski-slutna mängder i $\mathbb{F}^n$ visserligen är "små" i allmänhet (i bemärkelsen att deras komplement täcker nästan hela $\mathbb{F}^n$), men samtidigt beter sig lite "icke-kompakt" (den korrekta terminologin är att de inte är fullständiga varietéer).

Men man måste vara försiktig, för intuitionen om att Zariski-slutna mängder skulle bete sig "icke-kompakt" stämmer inte helt och hållet...

Det enklaste motexemplet är ändliga mängder, som ju verkligen är kompakta, men samtidgt är Zariski-slutna (vi har redan sett att enpunktsmängder är Zariski-slutna, och det är ganska lätt att utifrån det visa att alla ändliga mängder är slutna, se övningen nedan!).

Övning: Kan du hitta ett ekvationssytem i två variabler som har $\{(1,0),(0,1)\}$ (eller mer generellt: $\{(a,b),(c,d)\}$) som lösningsmängd? 

Ett annat problem som du själv är inne på är cirklar, ellipser och liknande objekt i $\mathbb{R}^2$, som också motsäger den här intuitionen (och kan hitta på liknnande saker i högre dimensioner). Men detta är en artifakt av att vi jobbar över en icke-algebraiskt sluten kropp. Jobbar vi över $\mathbb{C}$ (vilket man nästan alltid gör i klassisk algebraisk geometri) så försvinner de problemen.

Exempel: Mängden

   $\{(z,w)\in\mathbb{C}^2:z^2+w^2=1\}$

kommer att vara obegränsad i $\mathbb{C}^2$ (som vi geometriskt kan föreställa oss som $\mathbb{R}^4$). Hur stort $z$ vi än väljer, så kommer vi tack vara ett $\mathbb{C}$ är en algebraiskt sluten kropp (alltså tack vare algebrans fundamentalsats) kunna hitta något $w\in\mathbb{C}$ som gör att $z^2+w^2=1$ uppfylls. Om vi t.ex. drar till med $z=100$ så kan vi välja $w=i\sqrt{9999}$.

Mer precist gäller följande resultat:

Sats. Låt $X\subseteq\mathbb{C}^n$ vara en Zariski-sluten delmängd (alltså lösningsmängden till ett system av komplexa polynomekvationer i $n$ variabler). Då är $X$ antingen en ändlig mängd punkter eller obegränsad med avseende på den vanliga standardtopologin på $\mathbb{C}^n$.

Detta är ett förvånadsvärt djupt resultat, så till vida att påståendet är mycket enklare att förstå än beviset. De bevis jag känner till kräver antingen komplex analys (som inte är min starka sida) eller ett ganska tungt algebraiskt verktyg som kallas för Noether-normalisering...

Ja jag fattar sällan själv vad det är jag frågar om så det är ingen fara. Om du går in på wikipediasidan så kan du se att de skriver om topologiska vektorrum, i alla fall innan "statement of the theorem". Vad är det för skillnad mellan punkt 2 och 3? På sista raden där stasen skrivs ut så handlar det om vektorrum igen. 

Det där vill jag ställa en följdfråga om. Asså, topologi är en sak vi kan definiera på mängder (tex Zariski på $\mathbb{R}^n$). Om vi definierar (eller om det är inducerat av ngt) det på ett vektorrum så kallas det ett topologiskt vektorrum? Ja det verkar rimligt. Och nu har jag glömt bort min fråga.

Det låter som att vanliga icke-vektor topologiska rum är väldigt fattiga jämfört med topologiska vektorrum, stämmer det?

Är nog en ganska enkel övning att kontrollera detta om du går in och läser Wikipedia-artiklarna om alla kriterierna! ^_^

Kan jag göra det utan att komma på motexempel som du har gjort? Jag kan ingen topologi som du vet.

Om du inte redan har gjort det så är det bara en tidsfråga innan du stöter på något som har med projektiv geometri att göra! ^_^

Lägger det på minnet!

Övning: Kan du hitta ett ekvationssytem i två variabler som har {(1,0),(0,1)} (eller mer generellt: {(a,b),(c,d)} som lösningsmängd? 

Öh... Den har inga övriga krav? Isåfall (bx-ay)(dx-cy)=0? (antar jag kommutativitet?)

Men detta är en artifakt av att vi jobbar över en icke-algebraiskt sluten kropp.

Exakt! En gång sa du att linjär algebra med C är trevligt för att det är en algebraiskt sluten kropp, snart ska jag sätta igång med det.

De bevis jag känner till kräver antingen komplex analys (som inte är min starka sida) eller ett ganska tungt algebraiskt verktyg som kallas för Noether-normalisering...

Wow, bevis för en och samma sak från två vitt skilda (?) områden, fett coolt.

Edit: jag tittade på wiki, ojoj. Men vadå lemma?