Linjär algebra, Rotera avbildningsmatris kring två olika axlar. (J. Månsson 8.20)

Den första rotationen flyttar positiva y-axeln till positiva z-axeln och positiva z-axeln till negativa y-axeln, medan x-axeln blir kvar där den var från början. Stämmer detta med din matris?

Smaragdalena skrev:

Den första rotationen flyttar positiva y-axeln till positiva z-axeln och positiva z-axeln till negativa y-axeln, medan x-axeln blir kvar där den var från början. Stämmer detta med din matris?

Det är det jag (tänker) att jag har gjort och resultatet är "B" matrisen

Den positiva y-axeln är vektorn $(0,1,0)$ och den ska till den positiva z-axeln $(0,0,1)$.

Testa att rotera $(0,1,0)$ med din matris $B$. Får du verkligen (0,0,1)?

Kolonnerna i $B$ ska vara de roterade basvektorerna i tur och ordning. x-axeln lämnas orörd $(1,0,0)^T$, den andra kolonnen ska enligt ovan vara $(0,0,1)^T$ osv.

Har korrigerat mina beräkningar något: 

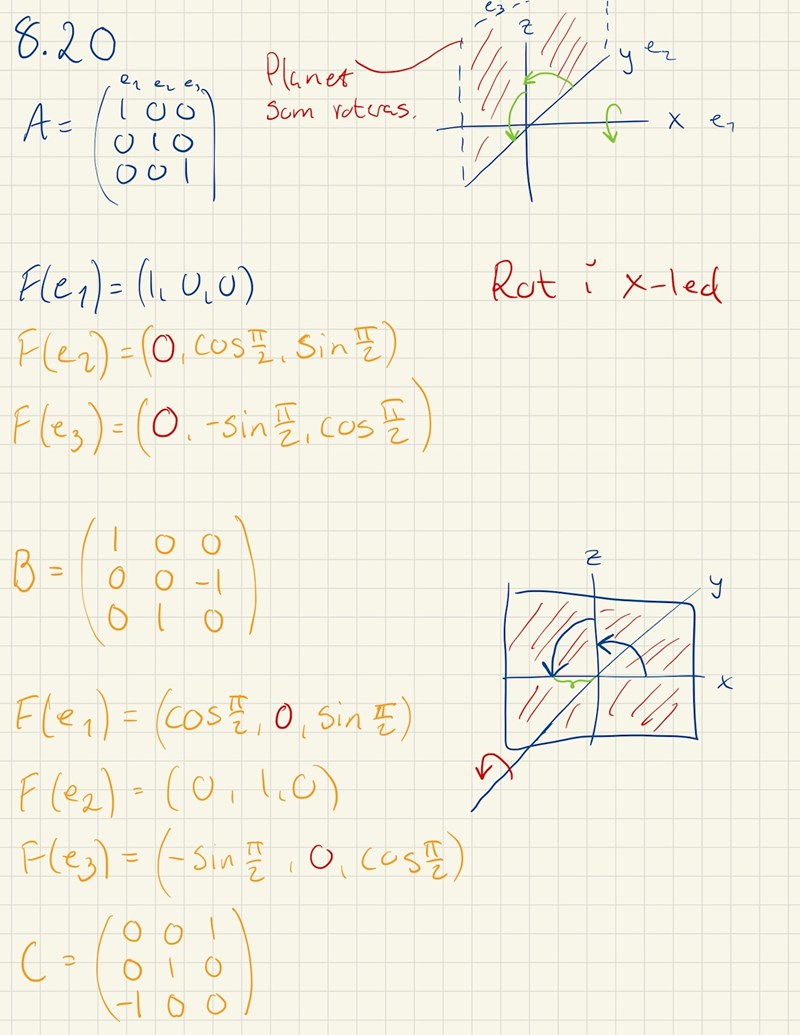
Vilket ger mig rätt resultat men i "omvänd ordning", men detta kanske kokar ner till att jag har en annan placering på mina x,y,z axlar? 

Bra, nu har du rätt rotationsmatriser, men tänk på hur matriserna verkar på en vektor $\mathbf{u}$

Om vi först roterar kring x-axeln får vi

$\mathbf{u}\prime=B\mathbf{u}$

Om vi sedan roterar den resulterande vektorn kring y-axeln får vi

$C\mathbf{u}\prime=C(B\mathbf{u})=CB\mathbf{u}$

En rotation kring x följt av en rotation kring y är alltså matrisen $CB$

D4NIEL skrev:

Bra, nu har du rätt rotationsmatriser, men tänk på hur matriserna verkar på en vektor $\mathbf{u}$

Om vi först roterar kring x-axeln får vi

$\mathbf{u}\prime=B\mathbf{u}$

Om vi sedan roterar den resulterande vektorn kring y-axeln får vi

$C\mathbf{u}\prime=C(B\mathbf{u})=CB\mathbf{u}$

En rotation kring x följt av en rotation kring y är alltså matrisen $CB$

aha! Tack ännu en gång! 

ChocolateTerrain skrev:

Har korrigerat mina beräkningar något: 

Vilket ger mig rätt resultat men i "omvänd ordning", men detta kanske kokar ner till att jag har en annan placering på mina x,y,z axlar? 

Hej igen! Försökte mig på denna uppgift idag igen då jag tänkte att jag hade förstått den till fullo. Men så verkar inte fallet vara. Mitt problem är vid transponeringen av "C" matrisen (som jag nu kallar "Y"):

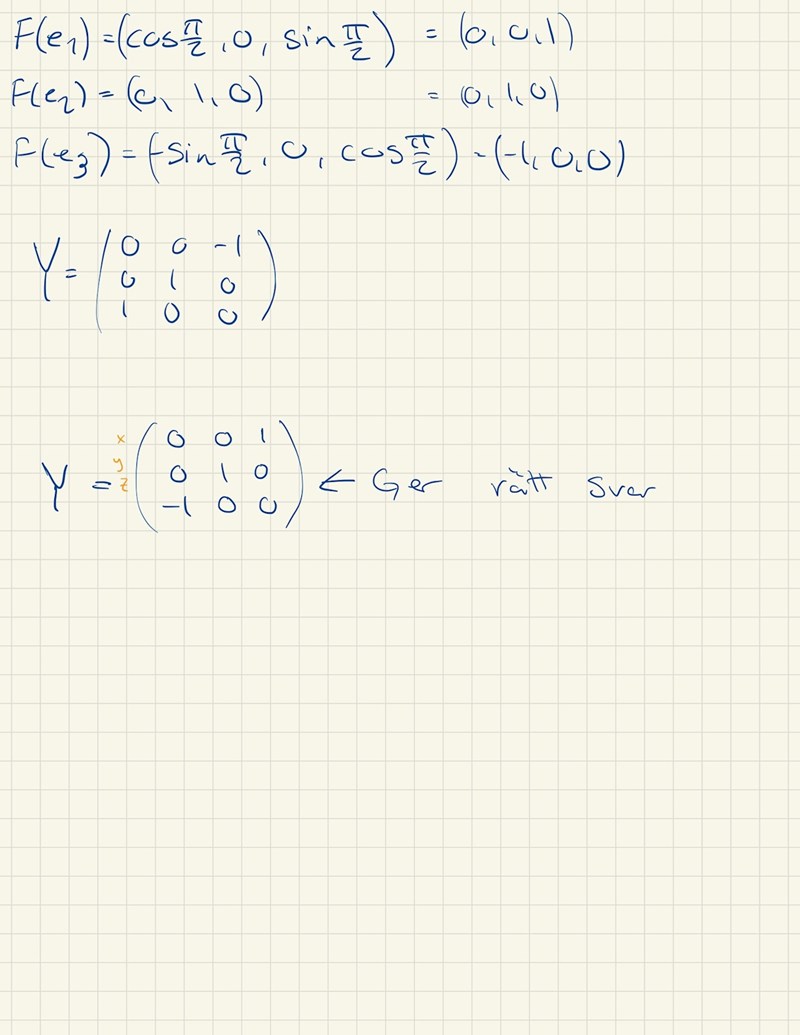
Kanske kan den här bilden hjälpa dig. Den vänstra bilden är koordinatsystemet sett ur perspektiv. Den högra bilden är samma koordinatsystem sett från spetsen av y-axeln. Notera att x-axeln pekar åt vänster.

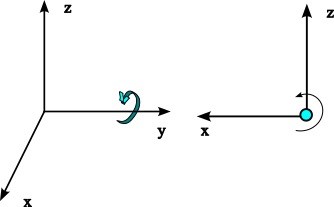
basvektor (1,0,0)  ska till (0,0,-1)

basvektor (0,1,0) lämnas oförändrad (rotation kring denna axel)

basvektor (0,0,1) ska till (1,0,0)

Det ger rotatationsmatrisen (för en rotation $\pi/2$ i positiv led kring y-axeln sett från spetsen av y-axeln)

$R_y=\left(\begin{array}{ccc}0 & 0 & 1 \\0 & 1 & 0 \\-1 & 0 & 0 \end{array}\right)$

D4NIEL skrev:

Kanske kan den här bilden hjälpa dig. Den vänstra bilden är koordinatsystemet sett ur perspektiv. Den högra bilden är samma koordinatsystem sett från spetsen av y-axeln. Notera att x-axeln pekar åt vänster.

basvektor (1,0,0)  ska till (0,0,-1)

basvektor (0,1,0) lämnas oförändrad (rotation kring denna axel)

basvektor (0,0,1) ska till (1,0,0)

Det ger rotatationsmatrisen (för en rotation $\pi/2$ i positiv led kring y-axeln sett från spetsen av y-axeln)

$R_y=\left(\begin{array}{ccc}0 & 0 & 1 \\0 & 1 & 0 \\-1 & 0 & 0 \end{array}\right)$

Okej! Tror jag börjar förstå det nu! (min egna beräkning:)

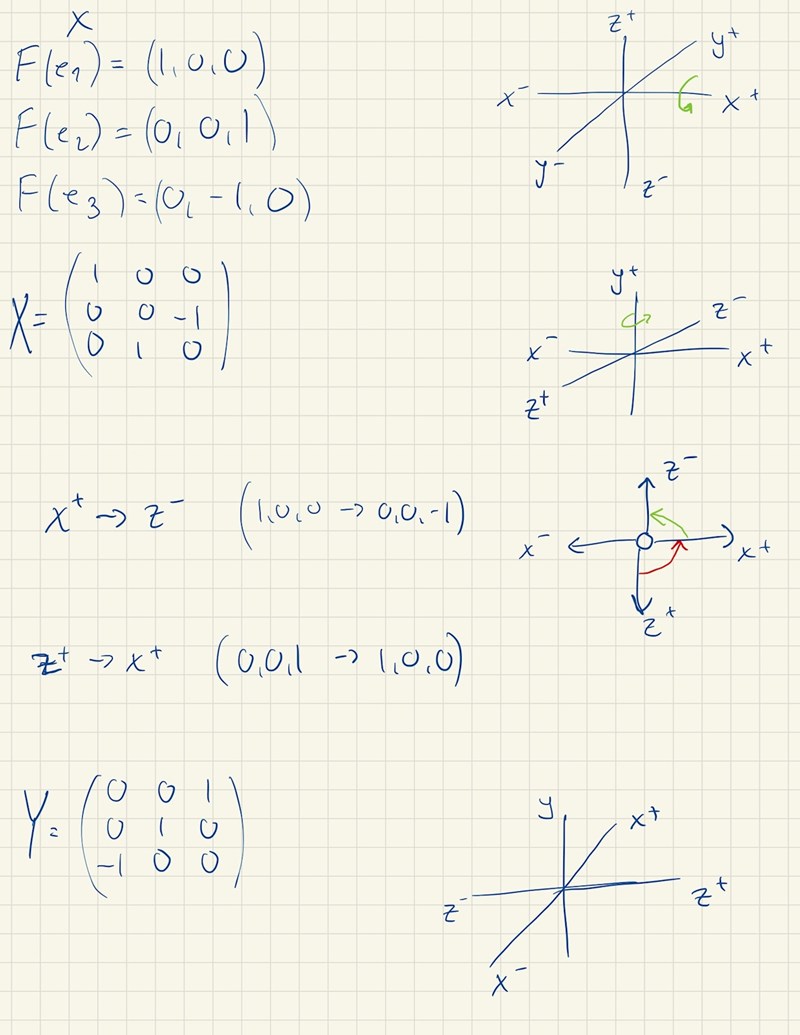
Men samtidigt så uppstår frågan om det är en annan vinkel än pi/2. Om det ex. är pi/3 i x-axeln följt av pi/6 i y-axeln?

Hur gör jag då?

I boken (vilket var det jag försökte göra när jag gjorde denna uppgift först) nämner de: 

Alltså, hur förändras cosv och sinv för rotation kring x och y-axeln? (hur ska avbindlingsmatrisen se ut)

Det är bara att projicera de "nya koordinataxlarna" på de gamla. För rotation kring x-axeln sett från spetsen av x-axeln ser det ut så här:

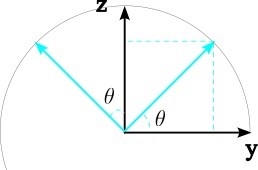
Vi ser att y-axeln ska till $(0,\cos(\theta),\sin(\theta))$

z-axeln ska till $(0,-\sin(\theta),\cos(\theta))$

x-axeln lämnas orörd, alltså blir rotationsmatrisen

$R_x=\left(\begin{array}{ccc}1 & 0 & 0 \\0 & \cos (\theta ) & -\sin (\theta ) \\0 & \sin (\theta ) & \cos (\theta ) \end{array}\right)$

För rotation kring y-axeln får vi på motsvarande sätt

$R_y=\left(\begin{array}{ccc}\cos (\theta ) & 0 & \sin (\theta ) \\0 & 1 & 0 \\-\sin (\theta ) & 0 & \cos (\theta ) \end{array}\right)$

Som minnesregel (om du inte vill räkna ut matriserna) kan du tänka på att först sätta in den axel som ska lämnas orörd och sedan placera ut mönstret för $\sin(\theta)$ och $\cos(\theta)$. Jag skulle dock rekommendera att du faktiskt gör en snabb skiss, det är väldigt lätt att råka göra ett teckenfel annars.

D4NIEL skrev:

Det är bara att projicera de "nya koordinataxlarna" på de gamla. För rotation kring x-axeln sett från spetsen av x-axeln ser det ut så här:

Vi ser att y-axeln ska till $(0,\cos(\theta),\sin(\theta))$

z-axeln ska till $(0,-\sin(\theta),\cos(\theta))$

x-axeln lämnas orörd, alltså blir rotationsmatrisen

$R_x=\left(\begin{array}{ccc}1 & 0 & 0 \\0 & \cos (\theta ) & -\sin (\theta ) \\0 & \sin (\theta ) & \cos (\theta ) \end{array}\right)$

För rotation kring y-axeln får vi på motsvarande sätt

$R_y=\left(\begin{array}{ccc}\cos (\theta ) & 0 & \sin (\theta ) \\0 & 1 & 0 \\-\sin (\theta ) & 0 & \cos (\theta ) \end{array}\right)$

Som minnesregel (om du inte vill räkna ut matriserna) kan du tänka på att först sätta in den axel som ska lämnas orörd och sedan placera ut mönstret för $\sin(\theta)$ och $\cos(\theta)$. Jag skulle dock rekommendera att du faktiskt gör en snabb skiss, det är väldigt lätt att råka göra ett teckenfel annars.

Tack återigen D4niel!