Linjär Algebra - skärningspunkter mellan två plan
Hej,
Jag har frågor om lösingsmetoder till uppgift 13.

Först testade jag att lösa uppgiften med substitutionsmetoden enligt nedan;
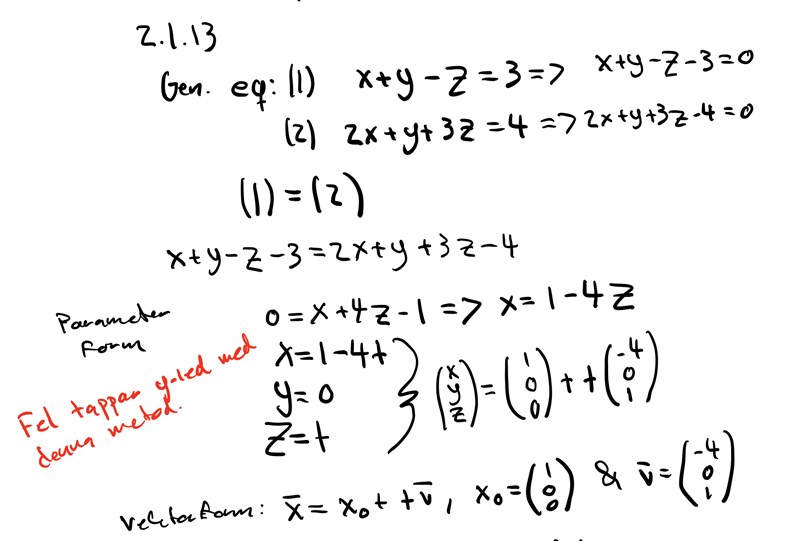
Som ni ser tappade jag y-led i denna metod då båda planensekvstion hade y=1, parameterlösningen för x och y blev rätt.
Sen testade jag att addera VL och HL men slutade direkt då jag förstod att det var fel - föratår dock inte varför.
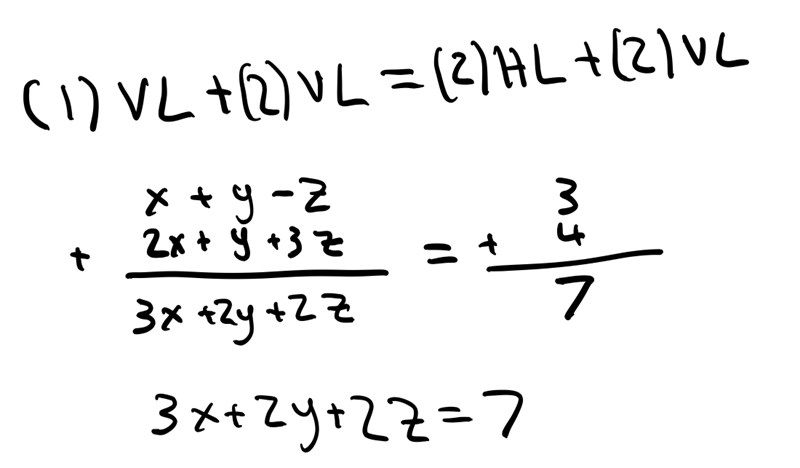
Sen insåg jag att jag sökte en gemensam lösning till ett ekvationsystemet som kan lösas med att Gaussa.
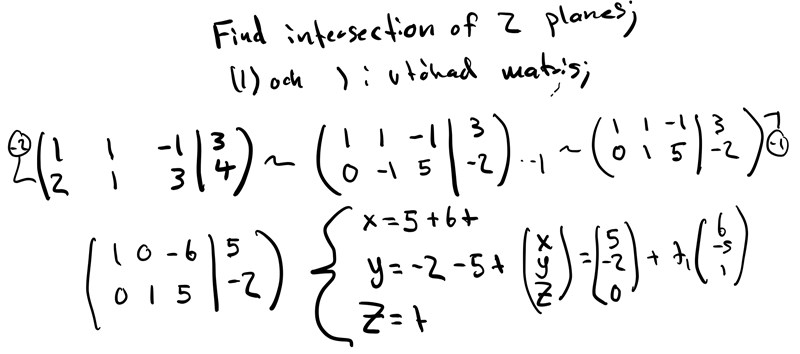
Men facit ger,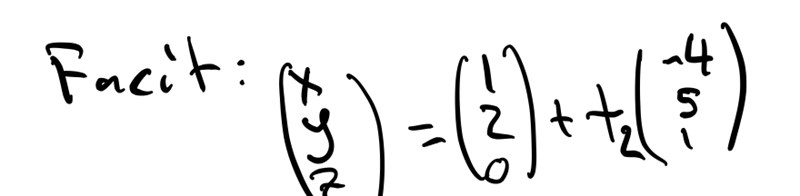
Jag försöker nu utreda ifall dessa två linjer kan skrivas om till samma. Då punkterna ligger i samma plan R3 - ligger de således på en linje enligt krav. Dock insåg jag att riktningsvektorerna är linjärt oberoende och de kan därför inte vara samma. Geogebra skissen visar även detta.

Har jag rätt ovh kan ni svara på mina olika lösningsmetoder om de bör fungera, vilka det finns och hur jag ska tänka när jag jämför med facit?
M V H
Twoface
Först o framst måste jag lika det för en sådant thorough utredning!
Jag som är slarvfel drottning kan berätta var slarvet har hänt:
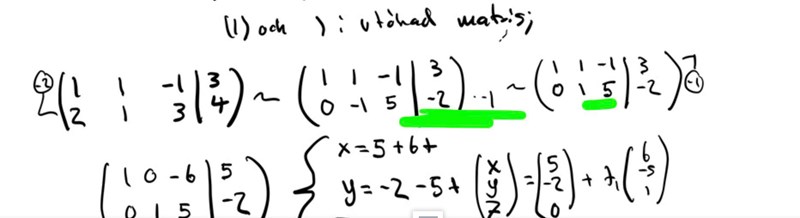
Fixar du det, får du rätt.
Tack för det!
Då konkluderar jag följande, gauss-jordan elimination var rätt strategi.
Min undre utredning var sannolikt korrekt då mitt slarvfel skapade en linjärt oberoende riktningsvektor till facits - vilket visas i geogebraskissen.
Men mina frågor kvarstår till varför strategi VL=HL alt Addera VL och HL inge fungerade alltså addition- och substitutionsmetoden som används i analysen. Den bör väl fungera men att lösningarna ges på generell form och inte parameterform direkt som guass eller gauss-Jordan gör?
Ingen av metoderna är fel, det är bara att du inte gör dem färdigt.
I den första löser du ut att x=1-4z och sedan hittar du på att y=0. Vad du i själva verket skall göra är att sätta tillbaka x=1-4z i antingen (1) eller (2). Om du sätter in det i (1) erhålles:
1-4z+y-z=3
y-5z=2
y=2+5z
Således vet du att:
x=1-4z
y=2+5z
Låter du z=t får du en parametrisering av linjen:
{x=1-4zy=2+5tz=taaaa
I den andra metoden kommer du fram till att:
3x+2y+2z=7
Här kan du exempelvis lösa ut att:
z=72-y-3x2
och sätta tillbaka i (1), vilket ger:
x+y-(72-y-3x2)=3
5x2+2y=132
2y=132-5x2
y=134-5x4
vilket ger:
z=72-(134-5x4)-3x2=14-x4
Om vi nu låter x=t får vi parametriseringen:
{x=taaaaay=134-5t4z=14-t4a
vilket är samma linje som förut.
Om du inte sätter tillbaka det du löser ut i en av ekvationerna blir resultatet att bara en av ekvationerna uppfylls, och därmed får du fel svar.



