Linjär algebra: tolkning av uppgift

Hej!

Här kommer en snabb fråga kring hur man ska tolka b)

Jag löste uppgiften och fick att $\vec x \notin V^{\perp}$ , samt att $\vec x \in V$ . (Följdfråga: nu dubbelkollade jag, men gäller att om $\vec x \notin V^{\perp} \implies \vec x \in V$ ? Nu kommer det jag inte förstår i uppgiften. Eller, visst förstår jag att $V$ består av två vektorer som kan spänna upp något slags plan och att speglingen i planet ges av $\vec x - 2\text{proj}_{\vec n}(\vec x)$ . Men, jag förstår inte vad uppgiften menar med definitionen $T(\vec x)=\vec x \text{ om } \vec x \in V, -\vec x \text { om } \vec x \in V^{\perp}$ , Den definitionen tolkar jag i fallet med den givna vektorn att eftersom $T(\vec x)=\vec x$ gäller $T(\begin{pmatrix}1\1\1\1\end{pmatrix})=T(\begin{pmatrix}1\1\1\1\end{pmatrix})$ . Men det är ju inte det en spegling är, och det är inte heller så den beräknas i facit... Vad menar de när de definierar $T$ så, och hur kan den definitionen vara ekvivalent med att $T$ beskriver en spegling i $V$ ?

Jag kan tyvärr inte på rak arm komma med ett fullständigt matematiskt svar. Men under tiden du väntar på att någon gör det kan jag försöka bidra med någon sorts intuition om din följdfråga och om att definitionen inte är orimlig genom tänka på denna situation men i R3 så att vi lättare kan visualisera. I R3 skulle ett exempel på situationen vara att V är ett plan. V* (som jag använder för att beteckna det ortogonala komplement eftersom jag skriver på telefonen) blir då linjen som är ortogonal mot planet. Prova att rita upp det.

Vi kan börja fundera på din följdfråga: kan du tänka dig en vektor som inte ligger i V* (dvs, inte är parallell med linjen) men som inte heller ligger i planet. Om du kan det så har du ett motexempel och den implikation som du skrivit gäller inte.

Om vi sedan tänker oss en spegling i V, det skulle i detta fall motsvara en spegling i planet. Vad händer med vektorer i V (dvs, vektorer i planet) när de speglas i V? Vad händer med vektorer i V* (dvs, vektorer parallell med linjen, ortogonala mot planet) när de speglas i V?

Ett tillägg: det jag beskrev ovan kanske kan ge lite mer intuition än vad jag tänkt.

Om du definierar en spegling som du gjort med x-2*proj(x på n), vad händer om x är en vektor i V? Vad händer om x är en vektor i V*? (Vektorn n är alltså en normal till V, dvs ortogonal mot V, så den ingår alltså i V*. Vad händer om du projicerar en vektor i V respektive V* på en vektor i V*?)

Hondel skrev:
Jag kan tyvärr inte på rak arm komma med ett fullständigt matematiskt svar. Men under tiden du väntar på att någon gör det kan jag försöka bidra med någon sorts intuition om din följdfråga och om att definitionen inte är orimlig genom tänka på denna situation men i R3 så att vi lättare kan visualisera. I R3 skulle ett exempel på situationen vara att V är ett plan. V* (som jag använder för att beteckna det ortogonala komplement eftersom jag skriver på telefonen) blir då linjen som är ortogonal mot planet. Prova att rita upp det.

Vi kan börja fundera på din följdfråga: kan du tänka dig en vektor som inte ligger i V* (dvs, inte är parallell med linjen) men som inte heller ligger i planet. Om du kan det så har du ett motexempel och den implikation som du skrivit gäller inte.

Om vi sedan tänker oss en spegling i V, det skulle i detta fall motsvara en spegling i planet. Vad händer med vektorer i V (dvs, vektorer i planet) när de speglas i V? Vad händer med vektorer i V* (dvs, vektorer parallell med linjen, ortogonala mot planet) när de speglas i V?

Tack så jättemycket för din input! Det första triviala exemplet jag kom att tänka på $xy$ -planet med $n=\hat k$ , dvs då ges $V$ av (till exempel) $span{(1,0,0),(0,1,0)}$ och $V^{\perp}$

av $span{(0,0,1)}$ . I min lärobok står följande:

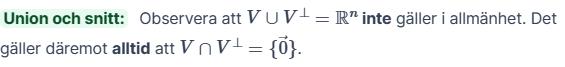
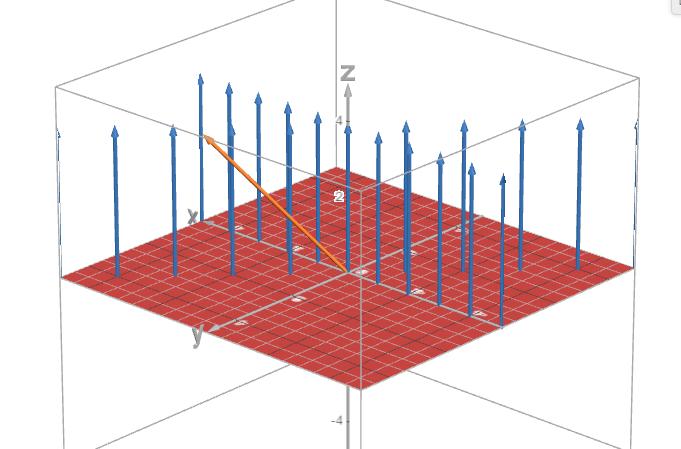
Men här ritade jag iallafall upp mitt exempel med lite vektorer utplacerade hipp som häpp. Jag tänkte att dessa är *några exempel* på vad som är med i $V^{\perp}$ :
Om jag då tänker mig en vektor som inte är i $xy$ -planet och inte vinkelrät mot det, har jag då hittat ett motexempel? Till exempel vektorn $(2,3,4)$ (den orangea vektorn):

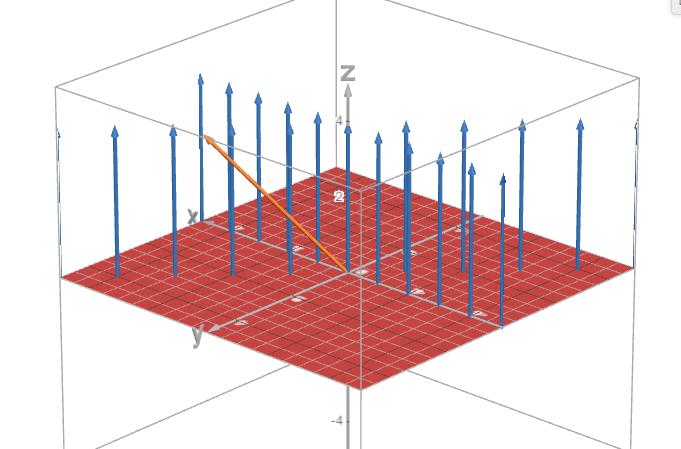
Och jag tror jag förstår vad som menas med speglingen nu! Om man tänker utifrån sättet jag och facit definierat speglingen så gäller mycket väl att $T(\vec x)=\vec x$ och $x\in V$ (eftersom $\text{proj}_{\vec n}(\vec x)=\vec 0$ och $x\in V^{\perp}$ ger att $T(\vec x)=-\vec x$ eftersom vektorerna speglas vinkelrätt mot planet.

Tack så mycket för att du satte igång lite tankar, så länge jag tänkt rätt med mitt motexempel ovan hänger jag med nu!

Varje vektor $\vec{v}$ $\in ℝ^{4}$ kan skrivas som en unik summa av en vektor $\vec{u}$ $\in V$ och en vektror $\vec{w} \in V^{⊥}$ . $\vec{v} = \vec{u} + \vec{w}$ .

Man säger att $ℝ^{4}$ är den direkta summan av V och V^$⊥$. Vilket brukar skrivas $ℝ^{4} = V \oplus V^{⊥}$ . Bekant?

Om detta inte är känt så kan du visa det med Gram-Schmidt.

Man kan nu definiera projektionsoperatorer enligt

$p r o j_{V} (\vec{v}) = \vec{u}$

$p r o j_{V^{⊥}} (\vec{v}) = \vec{w}$ .

Det brukar vara en övning att visa att detta definierar linjära avbildningar.

Således gäller det generellt att

$\vec{v} = p r o j_{V} (\vec{v}) + p r o j_{V^{⊥}} (\vec{v})$ (1).

Med att spegla en vektor $\vec{v}$ i V så menar man att man byter tecken på den del som är i det ortogonala komplementet. Dvs

$T (\vec{v}) = p r o j_{V} (\vec{v}) - p r o j_{V^{⊥}} (\vec{v})$ (2).

Om vi kombinerar (1) och (2) så får vi

$T (\vec{v}) = 2 p r o j_{V} (\vec{v}) - \vec{v}$ (3).

coffeshot skrev:
Hondel skrev:
Jag kan tyvärr inte på rak arm komma med ett fullständigt matematiskt svar. Men under tiden du väntar på att någon gör det kan jag försöka bidra med någon sorts intuition om din följdfråga och om att definitionen inte är orimlig genom tänka på denna situation men i R3 så att vi lättare kan visualisera. I R3 skulle ett exempel på situationen vara att V är ett plan. V* (som jag använder för att beteckna det ortogonala komplement eftersom jag skriver på telefonen) blir då linjen som är ortogonal mot planet. Prova att rita upp det.

Vi kan börja fundera på din följdfråga: kan du tänka dig en vektor som inte ligger i V* (dvs, inte är parallell med linjen) men som inte heller ligger i planet. Om du kan det så har du ett motexempel och den implikation som du skrivit gäller inte.

Om vi sedan tänker oss en spegling i V, det skulle i detta fall motsvara en spegling i planet. Vad händer med vektorer i V (dvs, vektorer i planet) när de speglas i V? Vad händer med vektorer i V* (dvs, vektorer parallell med linjen, ortogonala mot planet) när de speglas i V?

Tack så jättemycket för din input! Det första triviala exemplet jag kom att tänka på $xy$ -planet med $n=\hat k$ , dvs då ges $V$ av (till exempel) $span{(1,0,0),(0,1,0)}$ och $V^{\perp}$

av $span{(0,0,1)}$ . I min lärobok står följande:

Men här ritade jag iallafall upp mitt exempel med lite vektorer utplacerade hipp som häpp. Jag tänkte att dessa är *några exempel* på vad som är med i $V^{\perp}$ :
Om jag då tänker mig en vektor som inte är i $xy$ -planet och inte vinkelrät mot det, har jag då hittat ett motexempel? Till exempel vektorn $(2,3,4)$ (den orangea vektorn):

Och jag tror jag förstår vad som menas med speglingen nu! Om man tänker utifrån sättet jag och facit definierat speglingen så gäller mycket väl att $T(\vec x)=\vec x$ och $x\in V$ (eftersom $\text{proj}_{\vec n}(\vec x)=\vec 0$ och $x\in V^{\perp}$ ger att $T(\vec x)=-\vec x$ eftersom vektorerna speglas vinkelrätt mot planet.

Tack så mycket för att du satte igång lite tankar, så länge jag tänkt rätt med mitt motexempel ovan hänger jag med nu!

Ja jag tycker du har tänkt rätt med den orangea vektorn. Den ingår varken i V eller V*, så därför gäller inte din implikation. Dock skulle jag säga att alla blåa vektorer är samma vektor, eftersom en vektor bara har en längd och en riktning. Var du sedan ”placerar” denna vektor spelar ingen roll.

Jag vill också understryka att detta var sett som en illustration för att försöka ge någon intuitivt känsla. Notera att konceptet gäller även i R4, eftersom om du projicerar en vektor i V på en vektor som är ortogonal mot V (vektorn n) blir projektionen 0, det gäller även i högre dimensioner.

Hej, jag har inte svarat på detta än! Jag fattar att det var en tolkning som bara gäller i $\mathbb R^3$ , men den hjälpte mig verkligen!

Angående direkt summa så ingick den inte i den grundkurs-liknande linjär algebra-kursen jag läst hittills. Jag förstår däremot projektionsoperatorerna och ska läsa vidare på direkt summa av eget intresse!

Tack hörni!

coffeshot skrev:
Hej, jag har inte svarat på detta än! Jag fattar att det var en tolkning som bara gäller i $\mathbb R^3$ , men den hjälpte mig verkligen!

Angående direkt summa så ingick den inte i den grundkurs-liknande linjär algebra-kursen jag läst hittills. Jag förstår däremot projektionsoperatorerna och ska läsa vidare på direkt summa av eget intresse!

Tack hörni!

Hm, jag skulle säga tvärtom: att den mentala bilden funkar även för andra rum än R3.

Svara

Visa senaste svar