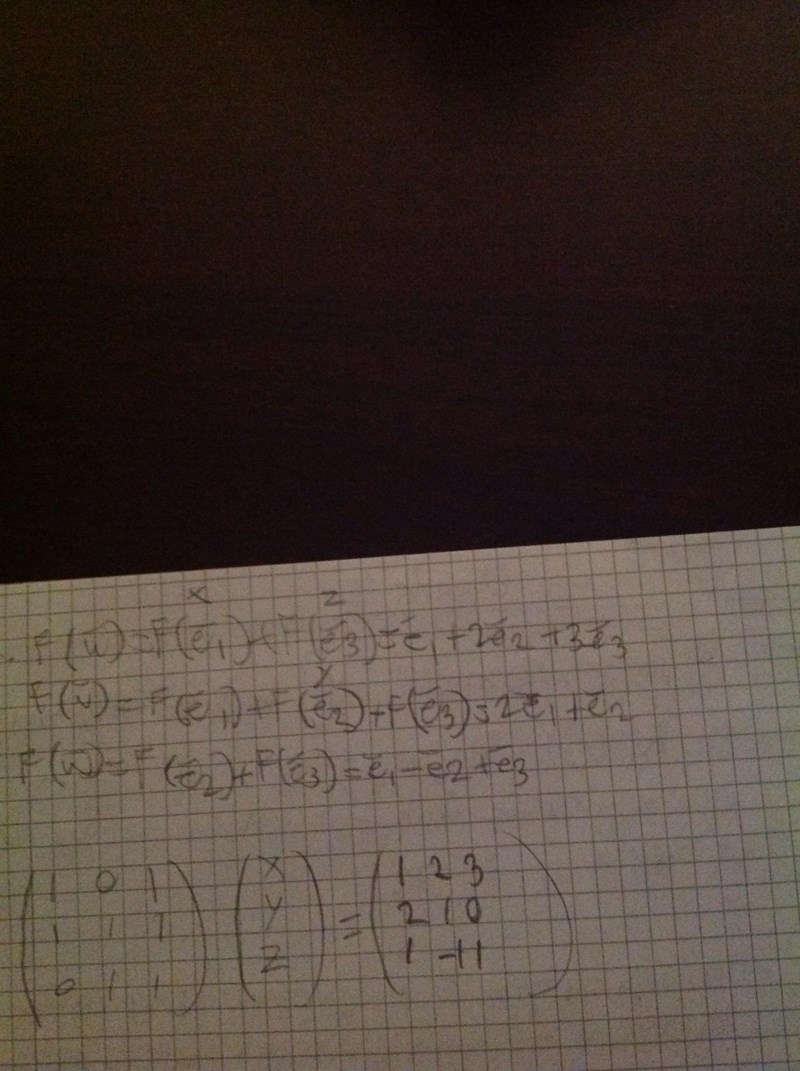24 svar

198 visningar

Linjär avbildning

Linjära avbildningen F: $R^{3} - > R^{3} d e f i n e r a s a v F (1, 0, 1) = (1, 2, 3), F (1, 1, 1) = (2, 1, 0), F (0, 1, 1) = (1, - 1, 1) . a) B e s t ä m F : s a v b i l d n i n g s m a t r i s i s \tan d a r d b a s e n . b) B e v i s a a t t d u h a r r ä t t g e n o m a t t a n v ä n d a d i n n y s s b e r ä k n a d e a v b i l d n i n g s m a t r i s t i l l a t t r ä k n a u t e t t a v d e o v a n g i v n a v ä r d e n a f ö r F .$

Jag vet inte riktigt hur jag ska lösa den men jag har gjort såhär: $(\begin{matrix} 1 & 0 & 1 \\ 1 & 1 & 1 \\ 0 & 1 & 1 \end{matrix}) (\begin{matrix} x \\ y \\ z \end{matrix}) = (\begin{matrix} 1 & 2 & 3 \\ 2 & 1 & 0 \\ 1 & - 1 & 1 \end{matrix}), x = F (e 1), y = F (e 2), z = F (e 3) F a s t n a r n ä r j a g s k a l ö s a d e n : \{\begin{cases} x 1 + x 3 = e 1 + 2 e 2 + 3 e 3 \\ y 1 + y 2 + y 3 = 2 e 1 + e 2 \end{cases} z 2 + z 3 = e 1 - e 2 + e 3$

Tacksam för hjälp!

Avbildningen är linjär. Du vet t.ex F(1,1,1) och F(1,0,1). Då har du att

F(0,1,0) = F(1,1,1) - F(1,0,1).

Dr. G skrev:
Avbildningen är linjär. Du vet t.ex F(1,1,1) och F(1,0,1). Då har du att
F(0,1,0) = F(1,1,1) - F(1,0,1).

aha så gäller du att F(1,1,1)-F(0,1,1)=F(1,0,0)? Eller?

För en linjär avbildning F gäller det alltid att

F(x + y) = F(x) + F(y)

där x och y är två godtyckliga vektorer.

I exemplet jag tog är x = (0,1,0) och y = (1,0,1), så x + y = (1,1,1).

Dr. G skrev:
För en linjär avbildning F gäller det alltid att
F(x + y) = F(x) + F(y)
där x och y är två godtyckliga vektorer.
I exemplet jag tog är x = (0,1,0) och y = (1,0,1), så x + y = (1,1,1).

Så jag kan göra så för att ta fram e1, e2 och e3?

Notationen är lite oklar. Är inte

e1 = (1,0,0)

e2 = (0,1,0)

e3 = (0,0,1)

d.v.s basvektorerna i standardbasen?

Dr. G skrev:
Notationen är lite oklar. Är inte
e1 = (1,0,0)
e2 = (0,1,0)
e3 = (0,0,1)
d.v.s basvektorerna i standardbasen?

jo, är lite förvirrad

Jag tog fram F(0,1,0), d.v.s F(e2).

Är du med på att det blir att F(0,1,0) = (1,-1,-3)?

Ta fram F(1,0,0) och F(0,0,1) på liknande sätt. Sedan kan avbildningens matris konstrueras.

Dr. G skrev:
Jag tog fram F(0,1,0), d.v.s F(e2).
Är du med på att det blir att F(0,1,0) = (1,-1,-3)?
Ta fram F(1,0,0) och F(0,0,1) på liknande sätt. Sedan kan avbildningens matris konstrueras.

Hur gör du när du övergår till (1,-1,-3)?

F(0,1,0) = F(1,1,1) - F(1,0,1) = (2,1,0) - (1,2,3) = (1,-1,-3)

Jag har använt linjäritet och två av de tre givna avbildningarna.

Dr. G skrev:
F(0,1,0) = F(1,1,1) - F(1,0,1) = (2,1,0) - (1,2,3) = (1,-1,-3)
Jag har använt linjäritet och två av de tre givna avbildningarna.

okej, varför går det att ta skillnaden mellan två linjära avbildningar för att få fram e1?

Och spelar det någon roll mellan vilka jag tar? tex F(0,1,1)-F(1,1,1)=(1,-1,1)-(2,1,0)=(-1,-2,1)?

Du har att

(0,1,0) = (1,1,1) - (1,0,1)

Då är

F(0,1,0) = F((1,1,1) - (1,0,1))

Eftersom F här är linjär gäller det att

F((1,1,1) - F(1,0,1)) = F(1,1,1) - F(1,0,1)

så alltså

F(0,1,0) = F(1,1,1) - F(1,0,1)

Möjligen skulle jag för tydlighets skull ha skrivit vektorerna som

[0,1,0]

och avbildningarna som

F([0,1,0])

etc.

EDIT: skrivfel ändrat

Dr. G skrev:
Du har att
(0,1,0) = (1,1,1) - (1,0,1)
Då är
F(0,1,0) = F((1,1,1) - F(1,0,1))
Eftersom F här är linjär gäller det att
F((1,1,1) - F(1,0,1)) = F(1,1,1) - F(1,0,1)
så alltså
F(0,1,0) = F(1,1,1) - F(1,0,1)

Möjligen skulle jag för tydlighets skull ha skrivit vektorerna som
[0,1,0]
och avbildningarna som
F([0,1,0])
etc.

Då tror jag att jag hänger med på det. Gör jag rätt då jag gör: F(0,1,1)-F(1,1,1)=(1,-1,1)-(2,1,0) och F(1,0,1)-F(0,1,1)=(1,2,3)-(1,-1,1)?

Det verkar inte fel, men är inte vad du vill få fram.

[1,0,0] = [1,1,1] - [0,1,1]

Du vet avbildningarna av båda vektorerna i HL.

[0,0,1] = [0,1,1] - [0,1,0]

Du vet avbildningen av den ena vektorn i HL och den andra avbildningen räknade vi ut.

Dr. G skrev:
Det verkar inte fel, men är inte vad du vill få fram.
[1,0,0] = [1,1,1] - [0,1,1]
Du vet avbildningarna av båda vektorerna i HL.
[0,0,1] = [0,1,1] - [0,1,0]
Du vet avbildningen av den ena vektorn i HL och den andra avbildningen räknade vi ut.

Varför går det att man använder (0,1,0) när man tar fram (0,0,1)?

För att

F([0,0,1]) =F([0,1,1]) - F([0,1,0])

Här råkar vi veta vad F([0,1,1]) är, då det är givet i uppgiften. F([0,1,0]) har vi tidigare räknat ut. Allt i HL är känt, så F([0,0,1]) trillar ut.

Ett annat exempel:

Om vi istället hade känt till F([2,2,1]) och F([1,1,0]) så hade vi använt att F([0,0,1]) = F([2,2,1]) - 2*F([1,1,0]), eftersom 2*F([1,1,0]) = F([2,2,0]).

I den här uppgiften vet vi hur tre linjärt oberoende vektorer i R3 avbildas. Då är avbildningen helt känd. Man kan via en linjärkombination av de kända avbildningarna få fram avbildningarna av basvektorerna, vilket jag har försökt visa här.

Dr. G skrev:
För att
F([0,0,1]) =F([0,1,1]) - F([0,1,0])
Här råkar vi veta vad F([0,1,1]) är, då det är givet i uppgiften. F([0,1,0]) har vi tidigare räknat ut. Allt i HL är känt, så F([0,0,1]) trillar ut.
Ett annat exempel:
Om vi istället hade känt till F([2,2,1]) och F([1,1,0]) så hade vi använt att F([0,0,1]) = F([2,2,1]) - 2*F([1,1,0]), eftersom 2*F([1,1,0]) = F([2,2,0]).
I den här uppgiften vet vi hur tre linjärt oberoende vektorer i R3 avbildas. Då är avbildningen helt känd. Man kan via en linjärkombination av de kända avbildningarna få fram avbildningarna av basvektorerna, vilket jag har försökt visa här.

Hur vet jag vad F(0,1,0) är efter avbildningen?

Dr. G skrev:
Du har att
(0,1,0) = (1,1,1) - (1,0,1)
Då är
F(0,1,0) = F((1,1,1) - (1,0,1))
Eftersom F här är linjär gäller det att
F((1,1,1) - F(1,0,1)) = F(1,1,1) - F(1,0,1)
så alltså
F(0,1,0) = F(1,1,1) - F(1,0,1)

Och för just den här linjära avbildningen så visste vi att

F(1,1,1) = (2,1,0)

F(1,0,1) = (1,2,3)

så alltså

F(0,1,0) = F(1,1,1) - F(1,0,1) = (2,1,0) - (1,2,3) = (1,-1,-3)

Dr. G skrev:
Dr. G skrev:
Du har att
(0,1,0) = (1,1,1) - (1,0,1)
Då är
F(0,1,0) = F((1,1,1) - (1,0,1))
Eftersom F här är linjär gäller det att
F((1,1,1) - F(1,0,1)) = F(1,1,1) - F(1,0,1)
så alltså
F(0,1,0) = F(1,1,1) - F(1,0,1)
Och för just den här linjära avbildningen så visste vi att
F(1,1,1) = (2,1,0)
F(1,0,1) = (1,2,3)
så alltså
F(0,1,0) = F(1,1,1) - F(1,0,1) = (2,1,0) - (1,2,3) = (1,-1,-3)

Okej, så då har jag alla? (1,2,-1),(1,-1,-3),(0,0,4)?

Hej!

Standardbasen i rummet utgörs av de tre vektorerna $e_{1}=(1,0,0)$ , $e_2=(0,1,0)$ och $e_3=(0,0,1)$ .

Du får veta följande:

$\displaystyle\begin{matrix}F(e_1+e_3) &=& e_{1}+2e_{2}+3e_{3}\\F(e_1+e_2+e_3)&=&2e_1+e_2\\F(e_2+e_3)&=&e_1-e_2+e_3\end{matrix}$

Yes!

F([1,0,0]) = F([1,1,1]) - F([0,1,1]) = [2,1,0] - [1,-1,1] = [1,2,-1]

F([0,0,1]) = F([0,1,1]) - F([0,1,0]) = [1,-1,1] - [1,-1,-3] = [0,0,4]

Avbildningens matris är då kolonnvektorerna

F([1,0,0]), F([0,1,0]), F([0,0,1])

efter varandra.

Testa att det är rätt genom att avbilda de givna vektorerna och se att avbildningarna stämmer.

Eftersom $F$ är en linjär avbildning så kan du utföra elementära radoperationer i det linjära vektor-ekvationssystemet.

Subtrahera Rad 1 från Rad 2 för att få

$\displaystyle F(e_2) = 2e_1+e_2-(e_1+2e_2+3e_3)=e_1-e_2-3e_3.$

Subtrahera Rad 3 från Rad 2 för att få

$F(e_1) = 2e_1+e_2-(e_1-e_2+e_3)=e_1+2e_2-e_3.$

Tillsammans med Rad 1 ger detta

$$\displaystyle F(e_3) = e_1+2e_2+3e_3-F(e_1) = e_1+2e_2+3e_3-(e_1+2e_2-e_3) = 4e_3$$.

Avbildningens matris i standardbasen är därför lika med

$\displaystyle\begin{pmatrix}F(e_1)&F(e_2)&F(e_3)\end{pmatrix} = \begin{pmatrix}1&1&0\\2&-1&0\\-1&-3&4\end{pmatrix}$

Vektorn $F(e_1+e_3)$ är lika med matrisprodukten

$\displaystyle\begin{pmatrix}1&1&0\\2&-1&0\\-1&-3&4\end{pmatrix}\begin{pmatrix}1\\0\\1\end{pmatrix} = \begin{pmatrix}1+0+0\\2+0+0\\-1+0+4\end{pmatrix}=\begin{pmatrix}1\\2\\3\end{pmatrix}$ .

Okej, tack verkar stämma! Går det att göra på ett till sätt genom att lösa den här matrisekvationen och få ut avbildningsmatrisen?

Svara

Visa senaste svar