Linjär kombination av vektorer!

Hej. Jag fick en uppgift med vektorer och linjära kombinationer:

I triangeln ABC, låt vara N den punkt på sidan BC som uppfyller villkoret $\left|CB\right|=4\left|CN\right|$, och låt X vara skärningspunkten mellan CM och AN, där M är mittpunkten av AB. Låt vidare $CN=\overrightarrow{u}$ och $BM=\overrightarrow{v}$. Uttryck CX i termer av $\overrightarrow{u}$ och $\overrightarrow{v}$. Beräkna $\frac{\left|CX\right|}{\left|CM\right|}$ och $\frac{Area(△ACX)}{Area(△ACM)}$.

Jag försökte skissa triangeln först. Sen ritade jag en parallell vektor till MB från spetsen C och en parallell vektor ME till BC från spetsen M.

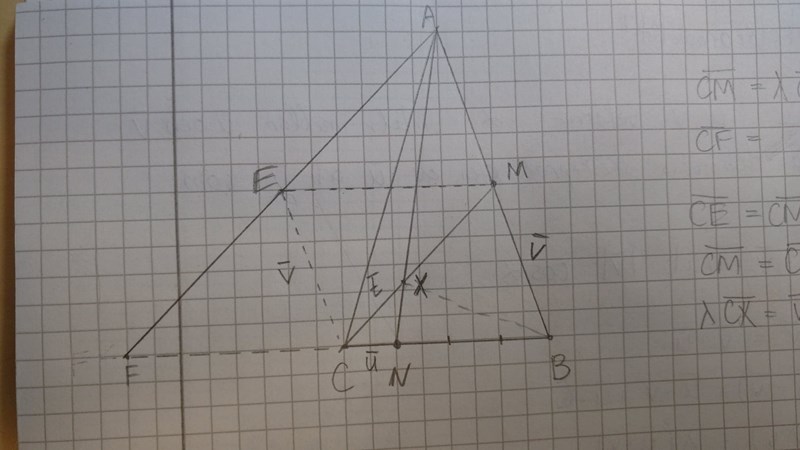
Som jag förstår så måste jag uttrycka vektor $\overline{CX}$som en linjär kombination av $\overrightarrow{u} och \overrightarrow{v}$ .

I boken står det bara en allmän lösning med konstanten $\lambda$ och enligt hänvisningarna fick jag

$$\begin{gathered} CM=\lambda *CX \\ \lambda *CX=4\overrightarrow{u}+(-\overrightarrow{v})=4\overrightarrow{u}-\overrightarrow{v} \end{gathered}$$

Men problemet är att jag fattar inte hur man ska hitta proportionen mellan CX och CM.

Jag tänkte också att jag borde använda faktum att CN=4CB och BM=1/2 BA och kom fram till

$$\begin{gathered} \overline{CN}=\overline{CA}+\overline{AN} \\ \overline{BN}=\overline{BA}-\overline{AM} \\ \overline{BN}=3\overline{NC}=3(-\overline{CN)}=-3\overline{CN} \\ \overline{BA}+\overline{AN}=-3\overline{CA}-3\overline{AN} \\ \overline{BA}=-3\overline{CA}-4\overline{AN} \end{gathered}$$

men kom ingenstans efteråt.

Vad har jag missat?

Tog bort fetstil (utom själva frågan) /Smaragdalena, moderator