Linjär regression, hjälp att förstå
Hej!
Jag skulle vilja veta hur enkel linjär regression fungerar men hittar ingen bra förklaring.
Jag är med på att det handlar om att hitta en linje där summan av de vertikala avstånden till varje punkt är så liten som möjligt, det känns intuitivt vettigt, men hur åstadkommer formeln
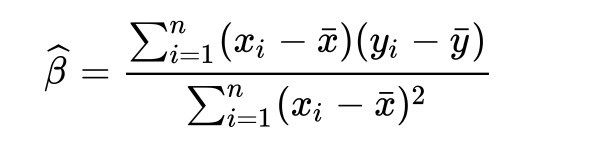 detta egentligen?
detta egentligen?
Vad är det som gör att vi får ”den bästa” lutningen genom att använda den här?
Det finns hur många sidor som helst på nätet som säger att denna minimerar residualerna men jag hittar ingen som förklarar varför.
Tänk att jag inte är bra på matte men jag skulle ändå vilja kunna förklara med ord varför formeln fungerar.
Jag är kanske inte smart nog för att förstå? :)
I ord så blir det nog tyvärr inte så mycket bättre än att med det där valet av lutning så kommer du få den linje som minimerar vertikala avståndet mellan linjen och de datapunkter du har.
Du kan såklart välja en annan lutning, men det där valet kommer alltså vara den "bästa" i avseendet att minimerar avståndet mellan linjen och punkterna. Varför det blir exakt det där uttrycket kan visas matematiskt, men å andra sidan låter det inte som att du vill ha hela härledningen
Det är väl de vertikala avstånden i kvadrat och summerat över alla datapunkter som minimeras?
Hondel skrev:I ord så blir det nog tyvärr inte så mycket bättre än att med det där valet av lutning så kommer du få den linje som minimerar vertikala avståndet mellan linjen och de datapunkter du har.
Du kan såklart välja en annan lutning, men det där valet kommer alltså vara den "bästa" i avseendet att minimerar avståndet mellan linjen och punkterna. Varför det blir exakt det där uttrycket kan visas matematiskt, men å andra sidan låter det inte som att du vill ha hela härledningen
Okej, ja det är ju just varför vi får den optimala lutningen med denna formel som är intressant. Har du härledningen någonstans så länka gärna, även om jag misstänker att den är för avancerad för mig att förstå. :)
tomast80 skrev:Det är väl de vertikala avstånden i kvadrat och summerat över alla datapunkter som minimeras?
Japp, det tror jag nog, men hur minimeras de? Formeln fungerar ju uppenbarligen men jag kan inte få någon känsla för varför den fungerar. :)
Om linjen inte skall vara y=kx+m utan bara y=kx blir det ganska enkelt att visa.
Då är vertikala avståndet från en punkt (x,y) till linjen helt enkelt y-kx, som kvadrerat blir y2 - 2kyx + x2
Det beror naturligtvis av vilket värde man väljer på k.
Summan av alla dessa kvadrater blir (Summan av alla y2) + k2 * (Summan av alla x2) - 2k * (Summan av produkten x*y för varje punkt)
Hur varierar den summan när vi varierar k? Derivera summan med avseende på k, så får du
2 * k * (Summan av alla x2) - 2 * (Summan av produkten x*y för varje punkt)
Sätt den derivatan till noll, så har du en formel som liknar den du har visat.
...och sedan är det "bara" att göra om samma sak med en linje y=kx+m
Bubo skrev:Om linjen inte skall vara y=kx+m utan bara y=kx blir det ganska enkelt att visa.
Då är vertikala avståndet från en punkt (x,y) till linjen helt enkelt y-kx, som kvadrerat blir y2 - 2kyx + x2
Det beror naturligtvis av vilket värde man väljer på k.Summan av alla dessa kvadrater blir (Summan av alla y2) + k2 * (Summan av alla x2) - 2k * (Summan av produkten x*y för varje punkt)
Hur varierar den summan när vi varierar k? Derivera summan med avseende på k, så får du
2 * k * (Summan av alla x2) - 2 * (Summan av produkten x*y för varje punkt)
Sätt den derivatan till noll, så har du en formel som liknar den du har visat.
...och sedan är det "bara" att göra om samma sak med en linje y=kx+m
Tack!
Ska försöka sätta mig in i svaret i helgen!


