Linjärt (o)beroende

Jag försökte först lösa ut M1:s basvektorer genom att utesluta alla ”löjliga” element och sedan beskriva M1 som ett lösningsrum. 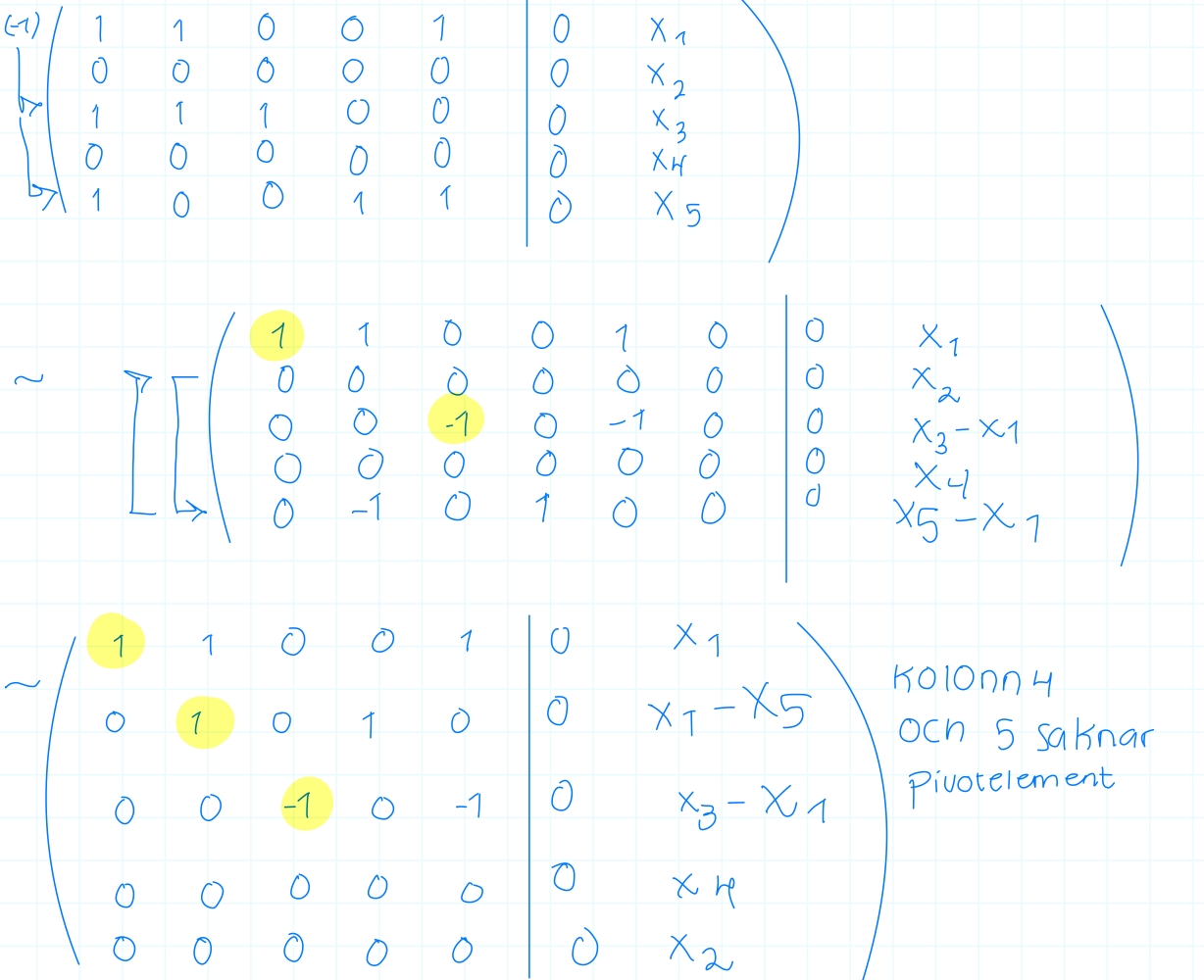
 Har jag gjort/tänkt rätt?
Har jag gjort/tänkt rätt?
Ingen?
Det var ett redigt bra tag sedan jag jobbade med sånt här. Jag blev tvungen att ta fram papper och penna och tänka efter själv varför det du kom fram till var riktigt trots att jag till en början ville hävda att du räknat fel. Du har gjort en del fel, men deras natur är sådana att jag gissar att du tänkt rätt men råkat skriva fel. Det jag försöker säga är att jag tror du har gjort rätt. Och att jag närapå inte begrep vad du gjort pga. felen.
Jag försökte först bilda en bas själv, eftersom jag inte förstod vad du gjorde:
M1 är noll i x2 och x4 för alla vektorerna. Tar man femte vektorn minus den fjärde får man (1,0,0,0,0). Den vektorn plus den tredje vektorn (0,0,1,0,0) och den fjärde vektorn (0,0,0,0,1) gör att en bas i M1 är {(1,0,0,0,0), (0,0,1,0,0), (0,0,0,0,1)} eftersom alla fem vektorerna kan beskrivas som en linjärkombination av dem.
Detta kom du också fram till, dvs. x2 = x4 = 0, övriga koordinater i M1 kan man röra sig fritt i.
Det första du gjorde var att sätta vektorerna i M1 som kolonner i en matris och därefter Gaussade du. Du måste fått fel på tredje raden; det tredje elementen borde vara 1, ej -1. I den mellersta matrisen råkade du även introducera en sjätte kolonn av nollor felaktigt.
Därefter kom du fram till att vid slutet av din Gaussning så fanns pivotelement till kolonn 1, 2, och 3, och därmed kunde de tre första vektorerna (1,0,1,0,1); (1,0,1,0,0); och (0,0,1,0,0) agera bas. Övriga var överflödiga och du kallade dessa för "löjliga". Du skrev dock felaktigt din andra basvektor som (1,0,0,1,0) ej (1,0,1,0,0).
Du lyckades sedan få till att en linjärkombination av (1,0,1,0,1); (1,0,1,0,0); och (0,0,1,0,0) kan beskrivas som att x2 och x4 är 0. Hur detta gick till vet jag dock inte, även om jag kan se att så är fallet med blotta ögat.
Okej jag insåg ganska sent att min lösning inte var så tydlig eller rätt för den delen. Här är en reviderad version

Det var så jag gjorde, och sedan ska jag väl göra samma sak för M2 och försöka komma fram till en bas och dimensionen för mängdernas snitt, med hjälp av att jag har uttryckt M1 och M2 som ett lösningsrum.
Låt mig tänka. För att övertyga mig själv.
Jag ignorerar nollorna i högerledet.
Du sätter upp att vektorn (x1,x2,x3,x4,x5) är en linjärkombination av vektorerna i M1.
Efter att du har gjort det kommer du fram till att om man räknar på detta så är det bl.a. samma sak som att hävda att x4 = 0+0+0+0+0 och x2 = 0+0+0+0+0, så för alla linjärkombinationer av vektorerna i M1 så blir andra och fjärde koordinaten 0.
Sedan kan man säga en del saker om värdena x1, x1-x5 och x1-x3, men det är inte relevant eftersom det inte begränsar M1:s rum. Jag blir här en smula förvirrad eftersom element 1 minus element 5 blir element 3, och element 1 minus element 3 blir element 5. Det väsentliga är att vi inte kan Gaussa bort några övriga rader utan att också Gaussa bort x-värdena i högerledet (om vi skulle ta rad III minus rad III så får vi förvisso en nollad rad men eftersom vi då tar x1-x3 minus x1-x3 så säger vi bara att 0=0, vi säger inte ett dyft om vilka begränsningar vi sätter på x1 och x3), vilket gör de essentiella bitarna i matrisen du Gaussat fram endast ligger i vilka rader som är nollade.
Om vi sedan tittar på nollorna i högerledet. Vi ignorerar nu x:en.
...bästa sättet för mig att komma underfund med det är att tänka på ett motexempel: antag att andra elementet hade varit samma som första, dvs. (1,0,1,0,1). Vill vi då använda första elementet i vår bas kommer andra elementet vara onödigt och dina uträkningar skulle i så fall visa det.
Jag får att motsvarande uträkning blir att kolonn 2 blir helt nollad då du Gaussar bort elementen i första kolonnen med hjälp av första raden. Och att då du sedermera väljer pivotelement omöjligen kan välja ett element från andra kolonnen, vilket motsvarar att motsvarande element ej kan utgöra basvektor till rummet. Vad är tolkningen av det mha. dina nollor?
Jag lyckas inte grunna ut vad tolkningen blir, men motexemplet övertygar mig om att du har gjort rätt.
Jag vet inte om jag har förstått dig rätt, men det du undrar är kanske vad det egentligen betyder att vissa koordinater alltid blir noll, eller att vissa kolumner nollas när man Gaussar och hur det hänger ihop med basen.
Svaret är att när en kolumn nollas bort vid Gauss-elimination betyder det att den vektorn (alltså den kolumnen) är linjärt beroende av tidigare, så den behövs inte för att spänna upp rummet. Det är därför man inte får något pivotelement där.
Geometriskt: den tillför inget nytt, den pekar i samma riktning som de andra. Alltså behövs den inte i basen.
Det jag försöker göra är att hjälpa dig. Och för att göra det behöver jag övertyga mig själv om att det du gör är riktigt. För att se om det är riktigt. Och så verkar vara fallet.

