linjärt optimeringsproblem
Figuren visar ett möjligt område ABCD för ett linjärt optimeringsproblem.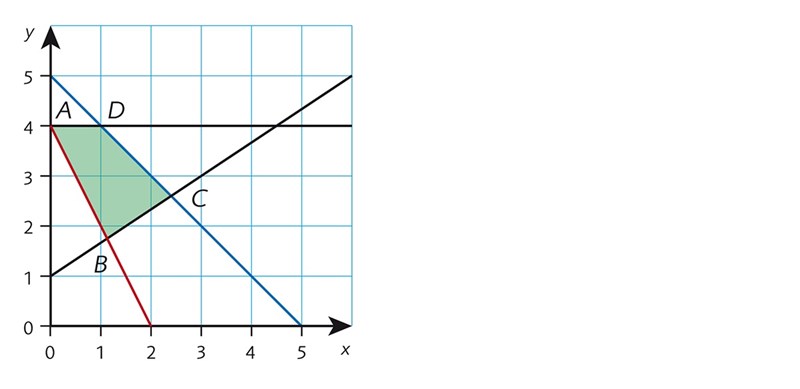
a) Skriv ner de olikheter som beskriver området.
b) Bestäm x och y så att funktionen F(x, y) = x + 2y får ett största värde.
c) I punkten B har funktionen y = kx + m ett minimum. Bestäm möjliga värden på konstanterna k och m.
Jag har ingen aning om hur jag ska gå tillväga här för att skriva ner de olikheter som beskriver området. Hur gör man det?
Enda olikheten jag vet är y < 4. Sedan vet jag inte hur jag ska göra längre än så.
Linjen y = kx + m delar in xy-planet i två delar.
För alla punkter ovanför linjen gäller olikheten y > kx + m
För alla punkter under linjen gäller olikheten y < kx + m
Kommer du vidare nu?
Nja alltså kan ju se ekvationen för de två linjerna som har y = -2x + 4 och
y = -x +5
Bra. Det är alltså AB och DC.
På vilken sida om dem ligger det möjliga området?
Och du hade ju AD redan, y = 6
På vilken sida om den ligger det möjliga området?
Återstår BC , som skär y-axeln i (0, 1)
Vad har den för lutning?
På vilken sida om den ligger det möjliga området?
AD: y = 4 , området ligger under linjen
AB: y = -2x + 4 , området ligger ovanför linjen
DC: y = -x +5 , området ligger under linjen
BC: y = 1,5x +1 , området ligger ovanför linjen
Men alltså jag förstår verkligen inte hur man kommer fram till svaret som ska vara:
y ≤ 4
2x+y−4 ≥ 0
x+y−5 ≤ 0
2x−3y+3 < 0
Skriv om begränsningslinjerna som ax + by + c = 0
Samma sak gäller även då, dvs
Linjen ax + by + c = 0 delar in xy-planet i två delar.
För alla punkter ovanför linjen gäller olikheten ax + by + c > 0
För alla punkter under linjen gäller olikheten ax + by + c < 0
Tillägg: 23 sep 2022 11:17
Det blev inte helt rätt här.
"Ovanför" ger då inte alltid > etc
Se rättelser i de två följande inläggen.
Ovanstående gäller om b > 0.
Om b < 0 så vänds olikheterna.
Specialfallet y = 0 delar istället in xy-planet i en vänster och en höger halva.
Tillägg: 23 sep 2022 10:21
Sorry, jag menar specialfallet b = 0 delar in xy-planet i en vänster och en höger halva.
Tack Yngve!
Jag borde ha skrivit så här:
Skriv om begränsningslinjerna som ax + by + c = 0 , om så erfordras.
Samma sak gäller även då, dvs
Linjen ax + by + c = 0 delar in xy-planet i två delar.
På den ena sidan om linjen gäller olikheten ax + by + c > 0
På den andra sidan om linjen gäller olikheten ax + by + c < 0
Skriver man begränsningslinjerna på k-form får olikheterna rätt tecken,
dvs ovanför linjen gäller > och under linjen gäller < .
Sedan kan man skriva om olikheterna om så krävs.
Då gäller de vanliga reglerna om olikheter.
För en vertikal begränsningslinje är det > till höger och < till vänster.
"Ovanför" är då alltså "i x-axelns riktning" etc.
ellenlindberg skrev:AD: y = 4 , området ligger under linjen
AB: y = -2x + 4 , området ligger ovanför linjen
DC: y = -x +5 , området ligger under linjen
BC: y = 1,5x +1 , området ligger ovanför linjen
Men alltså jag förstår verkligen inte hur man kommer fram till svaret som ska vara:
y ≤ 42x+y−4 ≥ 0
x+y−5 ≤ 0
2x−3y+3 < 0
Bra så långt!
Men du har råkat få fel riktning på den sista linjen
och även den olikheten ska väl vara av typen ≤ .
Då är du klar.
Resten är omformulering, om sådan krävs.
T ex AB: y = -2x + 4 , området ligger ovanför linjen
ger olikheten y ≥ -2x + 4 [eftersom även linjen tillhör det möjliga området]
som kan skrivas 2x + y - 4 ≥ 0 om så önskas.
Osv med övriga olikheter.
Linjen BC går genom punkterna (0,1) och (3,3). Det ger
Så BC blir .



