Linje i underrummet (LinAlg)

Hej!

Jag har lite frågor kring frågan:

Med lösningen:

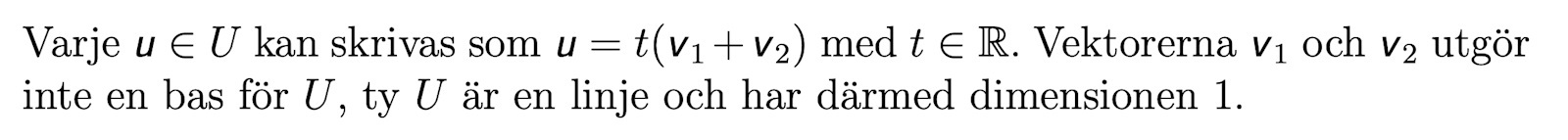
Jag undrar hur man kan se att U är en linje? Jag gissar att det har att göra med att z = 0, vilket gör att vi "plockar bort" den tredje dimensionen, men jag är inte säker.

Sedan att "x = y", innebär det att vi har en linje på samma vis som att vi hade skrivit in en linje i ett vanligt koordinatsystem där x-värdet alltid är lika med y-värdet?

Min sista fråga är hur vi kan skriva u = t(v1 + v2) och inte u = tv1 + sv2, d.v.s. att t =/= s. För en linjärkombination, som detta ju blir, behöver väl inte konstanterna framför vektorerna v1 och v2 vara likadana?

Jag tror att svaret på din sista fråga är nyckeln. Enligt definitionen av $U$ så gäller $x=y$ . Men $tv_1+sv_2=(t,s,0)$ , så för att ligga i U måste $t=s$ . Alltså är $U$ 1-dimensionellt (eftersom du kan skriva varje element i U som $u=tv=t(v_1+v_2)$ ), dvs en linje.

X=y är ett plan. Z=0 är ett plan. Punkter i U ska ligga i båda planen, dvs där de två planen skär. Det gör de i en linje. Alltså är U en linje.

haraldfreij skrev:
Jag tror att svaret på din sista fråga är nyckeln. Enligt definitionen av $U$ så gäller $x=y$ . Men $tv_1+sv_2=(t,s,0)$ , så för att ligga i U måste $t=s$ . Alltså är $U$ 1-dimensionellt (eftersom du kan skriva varje element i U som $u=tv=t(v_1+v_2)$ ), dvs en linje.

Tack så mycket för bra förklaring!

Hondel skrev:
X=y är ett plan. Z=0 är ett plan. Punkter i U ska ligga i båda planen, dvs där de två planen skär. Det gör de i en linje. Alltså är U en linje.

Tack Hondel!

Svara

Visa senaste svar