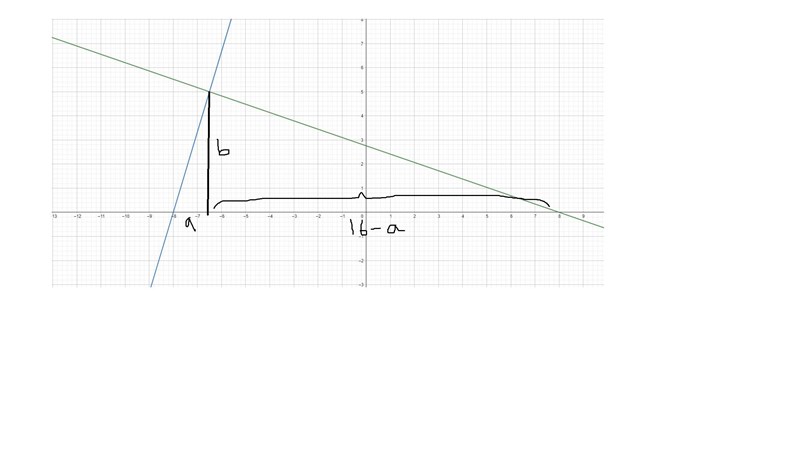
linje L
En triangel begränsas av x-axeln, linjen 10x + 29y − 80 = 0 och linjen L. Denna linje L går genom punkten (-8;0). Triangeln har arean 40 areaenheter.
Bestäm exakt ekvationen för linjen L
Linjerna jag får fram är
10x + 20y – 80 = 0 -> y = -0,5x + 4
y = 0
Tacksam för svar! men jag förstår inte varför det är så
https://www.pluggakuten.se/trad/triangel-i-ett-koordinatsystem-1 verkar vara samma fråga.
ja men jag förstår inte
Ser du att den andra punkten på x-axeln är (8,0). Hur skulle triangeln se ut? Vilken riktningskoefficient har den givna linjen och vad bör L ha för k för att det skall bli en triangel?
ingen aning asså kan du förklara varje steg på hur man gör
Om du sätter y= 0 i den givna ekvationen vad får du för x-värde? Och vad är k?
är det 8
Ja, så punkten är (8,0). Vad är riktningskoefficienten?
10?
Den räta linjens ekvation är y=kx+m om du jämför med y=-0,5x+4?
-0,5
Kan du rita in linjen i ett koordinatsystem?
det är det, jag vet inte hur
Ok här kommer bilden. Förstår du den?
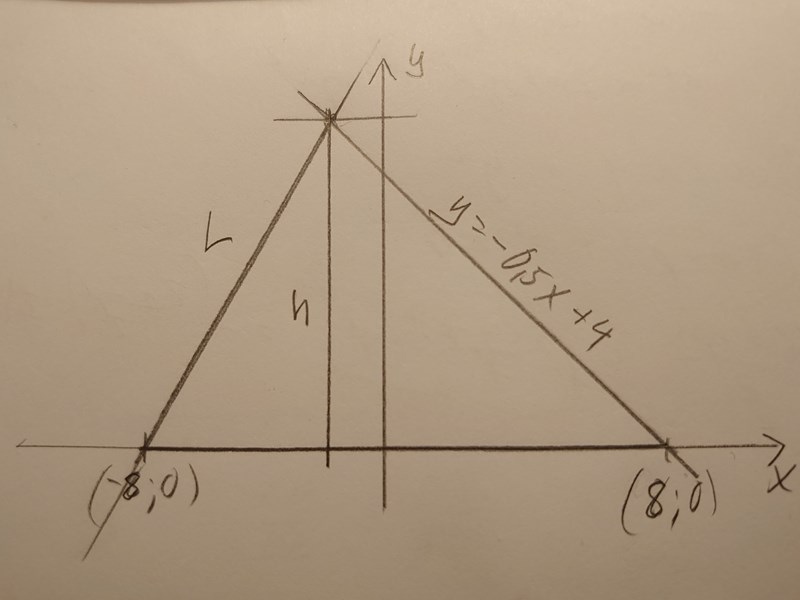
jaaa
Hur beräknar du höjden?
t upphöjt till2 gånger basen delat på 2
Ytan A=b*h/2. Hur lång är basen? Och hur stor är ytan enligt talet. Då kan du beräkna h
är basen 16
Ja basen är 16.
sen
Du fick ju formeln. A= bh/2. Sätt in det du vet och lös ut h.
Det finns ju faktiskt två linjer som är möjliga för att triangeln ska ha arean 40 a.e. Jag började med att ta reda på vart 10x+29-80=0 skar x-axeln, d.v.s. (8,0).
Låt sedan a beteckna avståndet från skärningspunkten mellan linjen L och 10x+29y-80=0, och skärningspunkten med linjen L och x-axeln. Låt b beteckna höjden på triangeln. Då kan man sätta upp en ekvation för arean av triangeln som ska bildas, förutsatt att k-värdet ska vara positivt på linjen L.
Med hjälp av höjden kan man sedan ta fram två punkter som linjen L ska gå igenom.
Förstår du?
Edvin Lake skrev:Det finns ju faktiskt två linjer som är möjliga för att triangeln ska ha arean 40 a.e. Jag började med att ta reda på vart 10x+29-80=0 skar x-axeln, d.v.s. (8,0).
Låt sedan a beteckna avståndet från skärningspunkten mellan linjen L och 10x+29y-80=0, och skärningspunkten med linjen L och x-axeln. Låt b beteckna höjden på triangeln. Då kan man sätta upp en ekvation för arean av triangeln som ska bildas, förutsatt att k-värdet ska vara positivt på linjen L.
Med hjälp av höjden kan man sedan ta fram två punkter som linjen L ska gå igenom.
Förstår du?
Linjen L skär ju x-axeln i (-8,0) enligt talet Jag kan inte se behovet av a. Basen längd är b=8-(-8)=16.
Däremot är det inte självklart vid första anblicken att linjerna korsas i 1:a eller 2:a kvadranten.
rapidos skrev:Edvin Lake skrev:Det finns ju faktiskt två linjer som är möjliga för att triangeln ska ha arean 40 a.e. Jag började med att ta reda på vart 10x+29-80=0 skar x-axeln, d.v.s. (8,0).
Låt sedan a beteckna avståndet från skärningspunkten mellan linjen L och 10x+29y-80=0, och skärningspunkten med linjen L och x-axeln. Låt b beteckna höjden på triangeln. Då kan man sätta upp en ekvation för arean av triangeln som ska bildas, förutsatt att k-värdet ska vara positivt på linjen L.
Med hjälp av höjden kan man sedan ta fram två punkter som linjen L ska gå igenom.
Förstår du?
Linjen L skär ju x-axeln i (-8,0) enligt talet Jag kan inte se behovet av a. Basen längd är b=8-(-8)=16.
Däremot är det inte självklart vid första anblicken att linjerna korsas i 1:a eller 2:a kvadranten.
Jo basens längd är 16, men eftersom att man inte vet skärningspunkten för linjerna behövs a om man ska göra en sådan uträkning som jag gjorde.
Edvin Lake skrev:rapidos skrev:Edvin Lake skrev:Det finns ju faktiskt två linjer som är möjliga för att triangeln ska ha arean 40 a.e. Jag började med att ta reda på vart 10x+29-80=0 skar x-axeln, d.v.s. (8,0).
Låt sedan a beteckna avståndet från skärningspunkten mellan linjen L och 10x+29y-80=0, och skärningspunkten med linjen L och x-axeln. Låt b beteckna höjden på triangeln. Då kan man sätta upp en ekvation för arean av triangeln som ska bildas, förutsatt att k-värdet ska vara positivt på linjen L.
Med hjälp av höjden kan man sedan ta fram två punkter som linjen L ska gå igenom.
Förstår du?
Linjen L skär ju x-axeln i (-8,0) enligt talet Jag kan inte se behovet av a. Basen längd är b=8-(-8)=16.
Däremot är det inte självklart vid första anblicken att linjerna korsas i 1:a eller 2:a kvadranten.
Jo basens längd är 16, men eftersom att man inte vet skärningspunkten för linjerna behövs a om man ska göra en sådan uträkning som jag gjorde.
Jag tänkte så här: höjden är vinkelrät mot basen, alltså motsvarar h=5 y-värdet för skärningspunkten. Därigenom får man x-värdet för skärningspunkten genom att sätta in y=5 i den kända linjen.
rapidos skrev:Edvin Lake skrev:rapidos skrev:Edvin Lake skrev:Det finns ju faktiskt två linjer som är möjliga för att triangeln ska ha arean 40 a.e. Jag började med att ta reda på vart 10x+29-80=0 skar x-axeln, d.v.s. (8,0).
Låt sedan a beteckna avståndet från skärningspunkten mellan linjen L och 10x+29y-80=0, och skärningspunkten med linjen L och x-axeln. Låt b beteckna höjden på triangeln. Då kan man sätta upp en ekvation för arean av triangeln som ska bildas, förutsatt att k-värdet ska vara positivt på linjen L.
Med hjälp av höjden kan man sedan ta fram två punkter som linjen L ska gå igenom.
Förstår du?
Linjen L skär ju x-axeln i (-8,0) enligt talet Jag kan inte se behovet av a. Basen längd är b=8-(-8)=16.
Däremot är det inte självklart vid första anblicken att linjerna korsas i 1:a eller 2:a kvadranten.
Jo basens längd är 16, men eftersom att man inte vet skärningspunkten för linjerna behövs a om man ska göra en sådan uträkning som jag gjorde.
Jag tänkte så här: höjden är vinkelrät mot basen, alltså motsvarar h=5 y-värdet för skärningspunkten. Därigenom får man x-värdet för skärningspunkten genom att sätta in y=5 i den kända linjen.
Precis, men för att få ut att h=5 kan man göra på mitt sätt och använda sig av a.
Edvin Lake skrev:rapidos skrev:Edvin Lake skrev:rapidos skrev:Edvin Lake skrev:Det finns ju faktiskt två linjer som är möjliga för att triangeln ska ha arean 40 a.e. Jag började med att ta reda på vart 10x+29-80=0 skar x-axeln, d.v.s. (8,0).
Låt sedan a beteckna avståndet från skärningspunkten mellan linjen L och 10x+29y-80=0, och skärningspunkten med linjen L och x-axeln. Låt b beteckna höjden på triangeln. Då kan man sätta upp en ekvation för arean av triangeln som ska bildas, förutsatt att k-värdet ska vara positivt på linjen L.
Med hjälp av höjden kan man sedan ta fram två punkter som linjen L ska gå igenom.
Förstår du?
Linjen L skär ju x-axeln i (-8,0) enligt talet Jag kan inte se behovet av a. Basen längd är b=8-(-8)=16.
Däremot är det inte självklart vid första anblicken att linjerna korsas i 1:a eller 2:a kvadranten.
Jo basens längd är 16, men eftersom att man inte vet skärningspunkten för linjerna behövs a om man ska göra en sådan uträkning som jag gjorde.
Jag tänkte så här: höjden är vinkelrät mot basen, alltså motsvarar h=5 y-värdet för skärningspunkten. Därigenom får man x-värdet för skärningspunkten genom att sätta in y=5 i den kända linjen.
Precis, men för att få ut att h=5 kan man göra på mitt sätt och använda sig av a.
Det är inte fel att göra så, men inte nödvändigt. Generellt gäller A=bh/2 oavsett formen på triangeln. Så 40=16*h/2 -> h=5