Linjeintegral med transformation från kartesiska till cylindriska koordinater
Hej!
2b) så har jag fastnat när det gäller att översätta från kartesiska till cylindriska koordinater. Ska man bara skriva om x uttryckt i cylindriska koordinater och multiplicera med första komponenten i detta fall bcos(s) och göra liknande för de andra termerna?

Generellt med cylinderkoordinater så gäller det att
.
Om du jämför det med parametriseringen så ser du att
z = b, .
Hjälper det?
PATENTERAMERA skrev:Generellt med cylinderkoordinater så gäller det att
.
Om du jämför det med parametriseringen så ser du att
z = b, .
Hjälper det?
Jag är med på att det är cylinderkoordinater med basvektorer ex , ey och ez. Men inte hur z=b , rho=b och phi=s blir på det sättet. Jag är inte heller på det här.
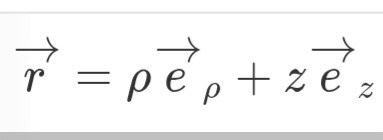
Jämför generella formeln med denna
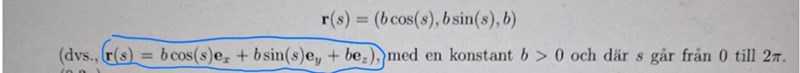
PATENTERAMERA skrev:Jämför generella formeln med denna
x=bcos(s)ex=rhocos(phi)ex => b=rho, s=phi
y=bsin(s)ey=rhosin(phi)ey => b=rho , s=phi
z=bez=zez => z=b
Men sen ska vi ju ha erho, ephi och ez. Hur får man till dem?
PATENTERAMERA skrev:
Varför är phi komponenten inte med för ortsvektorn r? Chatgpt får det till r(s)=bcos(2s)e_r+bsin(2s)e_phi+be_z.


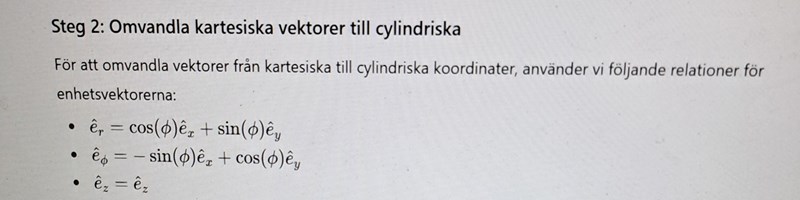
Ser ut som du gör teckenfel.

PATENTERAMERA skrev:Ser ut som du gör teckenfel.
Ja eller det är AI:s fel. Men det går alltså göra på det sättet och få då fram rätt transformering till cylindriska mha detta metod?
Tänk på att du kan alltid gå tillbaka till algebran.
Osv.
PATENTERAMERA skrev:Tänk på att du kan alltid gå tillbaka till algebran.
Osv.
Okej men vad blir ex skalärt med erho och samma sak med andra termen? Blir det inte bara 1 ifall ex och eho är ortogonala och ex och ephi?
destiny99 skrev:PATENTERAMERA skrev:Ser ut som du gör teckenfel.
Ja eller det är AI:s fel. Men det går alltså göra på det sättet och få då fram rätt transformering till cylindriska mha detta metod?
Ja det är väl bara att korrigera och räkna om. Men detta känns som att gå över ån för att hämta vatten. Det är ju bara att titta på uttrycken och jämföra.
destiny99 skrev:PATENTERAMERA skrev:Tänk på att du kan alltid gå tillbaka till algebran.
Osv.
Okej men vad blir ex skalärt med erho och samma sak med andra termen?
Cosinus för mellanliggande vinkel.
PATENTERAMERA skrev:destiny99 skrev:PATENTERAMERA skrev:Tänk på att du kan alltid gå tillbaka till algebran.
Osv.
Okej men vad blir ex skalärt med erho och samma sak med andra termen?
Cosinus för mellanliggande vinkel.
menar du att man ska ta skalärprodukten mellan ex och erho , sen ex och ephi och sen ey med erho och sen med ephi? Jag försökte med det men det gick ej så bra. Jag får inte mer än såhär ex*ephi=cos(alfa) osv. Hur vet jag att ex är uttryckt i e_r ?
Du fick formeln för ex i #10. Formeln för ey är helt analog.
PATENTERAMERA skrev:Du fick formeln för ex i #10. Formeln för ey är helt analog.
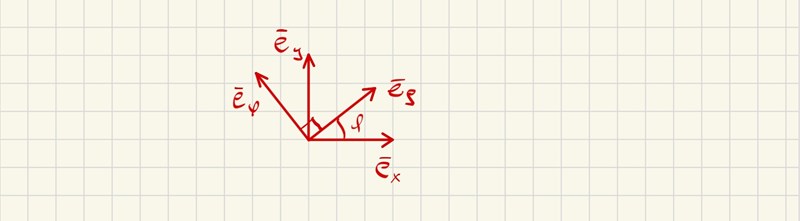
Jag har alltid undrat hur du formar den formeln. För jag kan inte skapa en liknande. Jag försökte tänka att e_rho är summan av e_phi och e_x utifrån din figur
PATENTERAMERA skrev:
Om jag förstår detta rätt så vill man skriva om ex som en linjärkombination av ephi och erho?
PATENTERAMERA skrev:Du fick formeln för ex i #10. Formeln för ey är helt analog.
För ey=(ey*erho)*erho+(ey*ephi)*ephi?
Jepp.
PATENTERAMERA skrev:Jepp.
Hur blir det med dr/ds vid integreringen pga cylinderkoordinater?
PATENTERAMERA skrev:.
Jag förstår inte riktigt. Ska jag derivera r(s) när vi har transformerat till cylindriska koordinater?
Du har ju formeln för r(s) i problemtexten. Det är bara att derivera. Sedan ser man att resultatet blir enkelt uttryckt i cylinderkoordinater.
PATENTERAMERA skrev:Du har ju formeln för r(s) i problemtexten. Det är bara att derivera. Sedan ser man att resultatet blir enkelt uttryckt i cylinderkoordinater.
Okej men då var det väl bättre att derivera den först och sen överföra resultatet till cylindriska koordinater.
Det var det jag gjorde i #23.