Lite konstigt i min bok
Hej, i delkapitlet om Eulers polyederformel vill boken göra en distinktion mellan "plan sammanhängande graf" och "sammanhängande graf" för att förklara att polyederformeln endast funkar för plana sammanhängande grafer.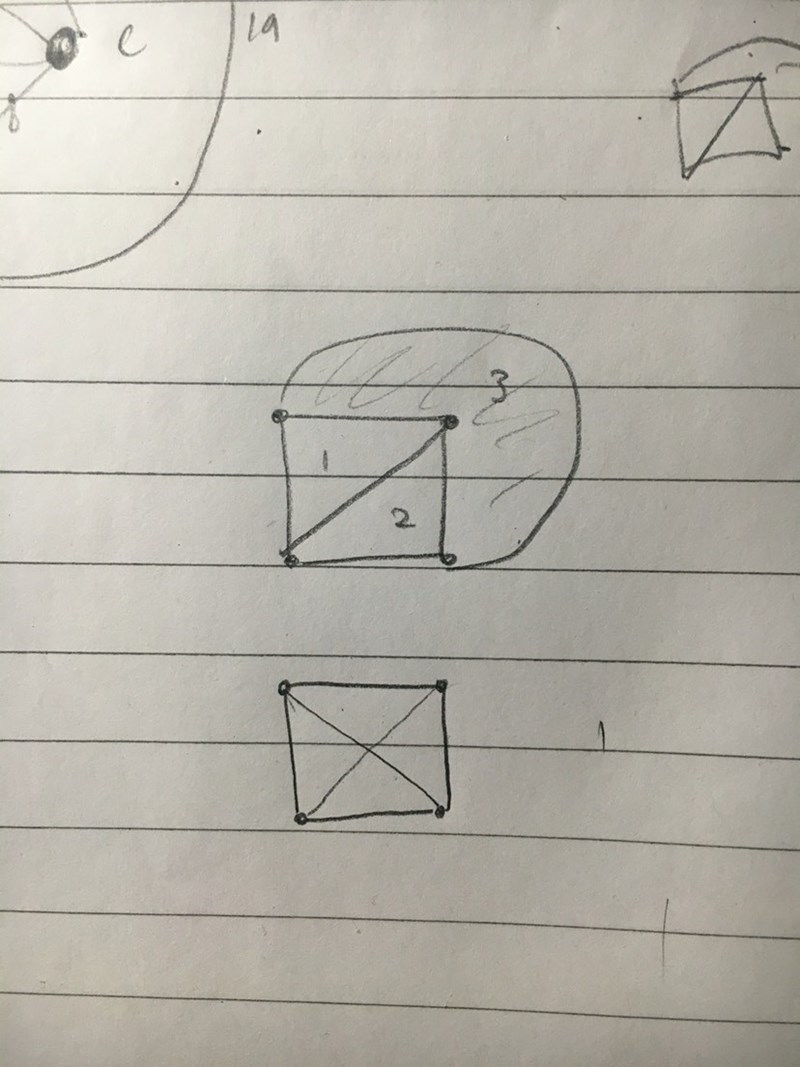 
Boken tar den nedre grafen som exempel på en icke-plan sammanhängande graf eftersom två kanter korsar varandra i mitten där. Jag förstår att det blir konstigt när man ska börja räkna ytor sen och att det är därför formeln inte funkar då, men om man bara makar på en av kanterna som jag har gjort i grafen ovanför så blir det ju en plan sammanhängande graf som formeln fungerar på, trots att det är precis samma graf. Dåligt exempel tycker jag.
Utmärkt exempel, anser jag. Dina två bilder är principiellt olika, eftersom det finns två kanter som korsar varandra i den nedre bilden men inte i den övre.
Hur definierar din bok "plan (sammanhängande) graf"? Är det nånting om att kanter inte får korsa varandra?
Den definierar inte det så explicit, men så som jag tolkar det får två kanter inte korsa såvida det inte är på ett hörn, då är den plan och sammanhängande.
Jag håller faktiskt inte med dig om att graferna är olika.
Under antagandet att en grafs planhet/oplanhet är en, för den specifika grafen, unik egenskap, måste två ekvivalenta grafer båda vara plana eller båda oplana. De två grafer jag har ritat är ekvivalenta, alltså är mitt antagande felaktigt och detta måste betyda att plan/oplan är en egenskap hos hur man valt att dra kanterna och inte egenskaper hos själva grafen.
Detta verkar vara alldeles för fult för att vara sant.
Skulle du säga att denna är principiellt olik de två andra?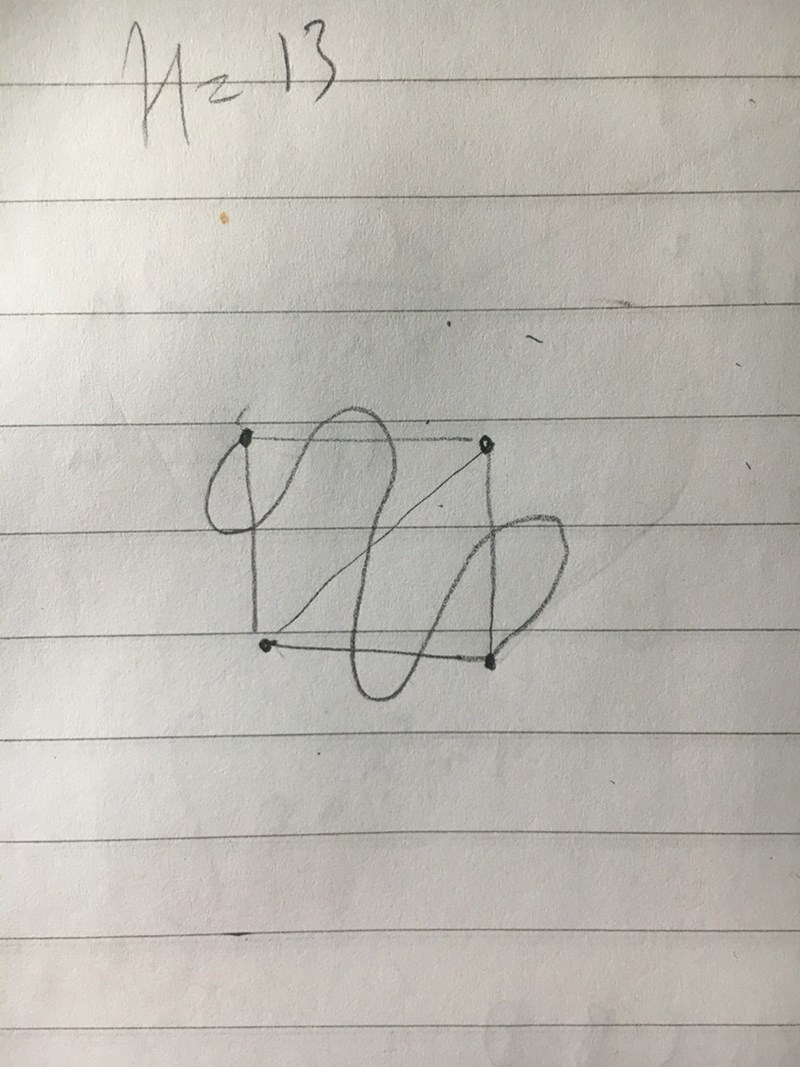
Vad betyder "principiellt olik"?
Den definierar inte det så explicit, men så som jag tolkar det får två kanter inte korsa såvida det inte är på ett hörn, då är den plan och sammanhängande.
Titta på din övre graf. Har den några korsningar?
Titta på din nedre graf. Har den några korsningar?
Kan en graf som har en korsning och en graf som inte har en korsning vara ekvivalenta?
Din nedre graf kan t ex föreställa en tetraeder. En tetraeder har fyra hörn, sex kanter och inga korsningar. En tetraeder är inte plan.
Smaragdalena skrev:Kan en graf som har en korsning och en graf som inte har en korsning vara ekvivalenta?
Ja.
Det är här vi inte kommer överens. Jag vet inte om jag har rätt.
Du har fel. En graf med en korsning är inte en plan graf, enligt definitionen som du själv har skrivit.
Smaragdalena skrev:Du har fel. En graf med en korsning är inte en plan graf, enligt definitionen som du själv har skrivit.
En graf med korsning är inte en plan graf, nej. Jag håller helt med.
Jag tror inte att jag har förmedlat min åsikt tillräckligt klart.
Jag tycker inte att en grafs egenskaper påverkas av hur jag som ritare ritar kanterna, hur lång kanten än är (om jag så tar min penna och ritar till umeå och tillbaka är det samma graf), vilka svängar den tar på vägen osv... Inget av det ska påverka.
Dessa fyra grafer är ekvivalenta: tycker inte du det?
Jag tycker att de är ekvivalenta eftersom det enda som skiljer de åt är hur jag har dragit kanten.
Smaragdalena skrev:Du har fel. En graf med en korsning är inte en plan graf, enligt definitionen som du själv har skrivit.
Enligt åtminstone en vanlig definition av graf (i s.k. grafteori) så har Qetsiyah rätt: då är en graf en mängd hörn och en mängd kanter, där en kant är ett par av hörn, och inget annat. Den har inget geometriskt i sig. Då visar de båda bilderna i början samma graf. En graf man kan rita i planet utan korsningar kallas planariserbar (eller planar), och att rita den utan korsningar kallas att planarisera den.
Om man ska representera polyedrar med grafer och få med sidorna på något sätt så måste man utöka definitionen.
Vad säger boken att definitionen på graf är?
Edit: kan du visa en bild på precis vad boken säger om plana grafer och det där som du skriver i början?
De är sparsamma med definitioner verkar det som (till skillnad från böckerna från 1c, 2c, 3 och 4 haha).
Jag håller med att någon sorts definitionsutökning är nödvändig.
Planariserbar och planarisera ska jag lägga på minnet.
Qetsiyah skrev:
De är sparsamma med definitioner verkar det som (till skillnad från böckerna från 1c, 2c, 3 och 4 haha).
Jag håller med att någon sorts definitionsutökning är nödvändig.
Planariserbar och planarisera ska jag lägga på minnet.
Om vi antar att de menar planariserade med plan, så har jag inget att anmärka på vad boken säger. De säger att en yta är "något" som helt omsluts av ett antal kanter (det som är utanför grafen ska också räknas som en yta), och det borde räcka om man inte är väldigt petig med definitioner.
Eulers formel uttrycker en relation mellan tre saker
Antal hörn
Antal kanter
Antal sidoytor
Medan de första två är grafteoretiska storheter så är de senare, sidoytorn, geometriska obkekt och kan inte räknas utan geometriska representationer och då behövs någon etablerad regel för hur man räknar dem så att antalet är oberoende att sättet man ritar bilden.
Hur räknar man sidoytor i en graf? Vad är ens sidoytor? Kan man räkna den utan en bild? Om du behöver en bild hur räknar du i bilden?
Går det att räkna ytor i bilden med de korsande kanterna? Jag tycker att det kanske går om man har en bra definition av vad en yta är i sammanhanget.
Laguna skrev:Qetsiyah skrev:De är sparsamma med definitioner verkar det som (till skillnad från böckerna från 1c, 2c, 3 och 4 haha).
Jag håller med att någon sorts definitionsutökning är nödvändig.
Planariserbar och planarisera ska jag lägga på minnet.
Om vi antar att de menar planariserade med plan, så har jag inget att anmärka på vad boken säger. De säger att en yta är "något" som helt omsluts av ett antal kanter (det som är utanför grafen ska också räknas som en yta), och det borde räcka om man inte är väldigt petig med definitioner.
Jag tycker att boken borde ta en icke-planiserbar graf (kan du rita en? Jag kan inte komma på någon...) som exempel, det vore allra tydligast.
Men då är planheten hos en graf inte en egenskap hos grafen utan en egenskap hos hur jag valt att rita den, eller hur?
Qetsiyah skrev:Laguna skrev:Qetsiyah skrev:De är sparsamma med definitioner verkar det som (till skillnad från böckerna från 1c, 2c, 3 och 4 haha).
Jag håller med att någon sorts definitionsutökning är nödvändig.
Planariserbar och planarisera ska jag lägga på minnet.
Om vi antar att de menar planariserade med plan, så har jag inget att anmärka på vad boken säger. De säger att en yta är "något" som helt omsluts av ett antal kanter (det som är utanför grafen ska också räknas som en yta), och det borde räcka om man inte är väldigt petig med definitioner.
Jag tycker att boken borde ta en icke-planiserbar graf (kan du rita en? Jag kan inte komma på någon...) som exempel, det vore allra tydligast.
Men då är planheten hos en graf inte en egenskap hos grafen utan en egenskap hos hur jag valt att rita den, eller hur?
Boken berättar om polyedrar och hur de kan representeras av vissa grafer. Då tillhör andra grafer än dessa inte ämnet.
En del grafer är inte planara. Ta t.ex. hörnen A, B, C och förbind alla dessa med alla hörnen D, E, F. Eller en annan graf: ta fem hörn och förbind alla med varandra.
https://youtu.be/xBkTIp6ajAg äntligen finns det här på numberphile!
