Lite lättare uppgift än 4.16
Många har tydligen tittat på mitt förra utlägg, utan att svara. Kanske tycker ni liksom jag att den här uppgiften är lättare att lösa. Här är det bara punkten 4 som jag inte kan skriva som en position. Jag har märkt ut var jag tror att punkterna ska vara, men punkt 4:s placering ser jag två möjliga ställen för. Var ska punkten vara och hur kan man motivera att punkten ska ha just den placeringen? Hur man kommer fram till x- och z-värdena för punkt 4 vet jag inte... 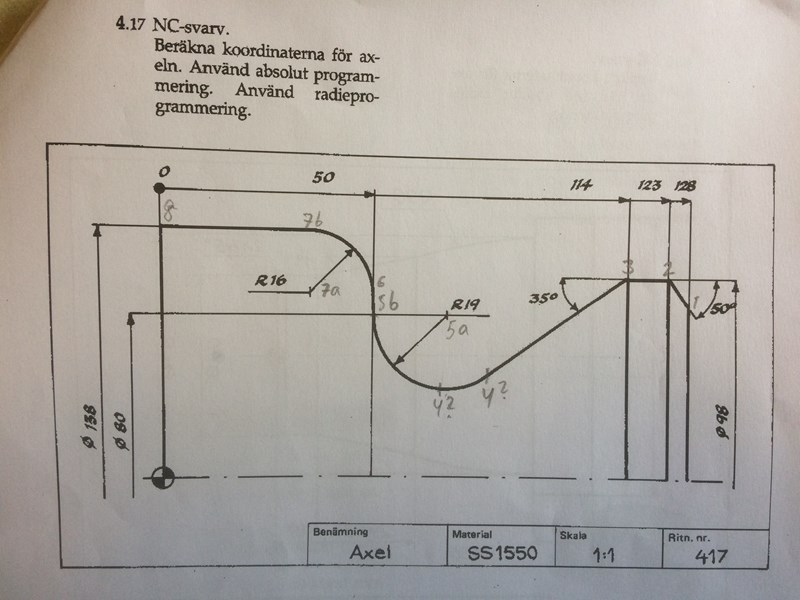
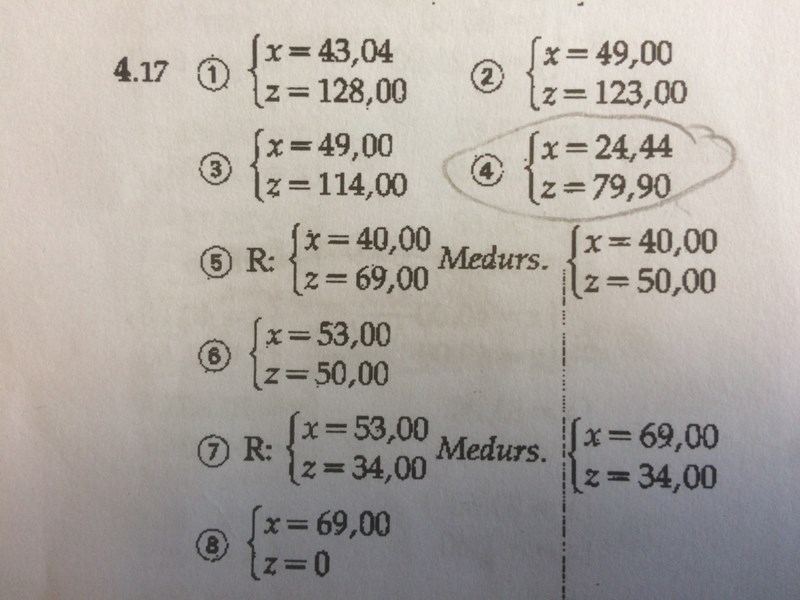
Jag får ta det här som en övning i geometri, för programmering av metallsvarv har jag aldrig sett förut.
Jag tror att punkt 4 är där det räta linjestycket från punkt 3 och neråt vänster med 35 grader slutar. Där börjar en cirkelbåge med centrum i 5a. För att hitta punkt 4 får man ta reda på var cirkelbågen lutar 35 grader uppåt, och det är där vinkeln mellan lodlinjen och linjen 5a-4 är 35 grader.
Det verkar bli lite algebra också, för vi verkar inte veta radien på cirkelbågen.
Tack för det Laguna!
Då beräknar jag Z-koordinaten i en tänkt triangel med hypotenusan mellan cirkelns medelpunkt och punkt 4 enligt följande:
Sin 35 grader = Z/19 (för ritningens radie tillika hypotenusan är 19).
Z är då ungefär lika med 10,898
Positionen horisontellt är då 50 + radien 19 + 10,898 = ungefär 79,90, dvs Z = 79,90.
X-värdet som i svarvsammanhang är den vertikala (lodräta) positionen lyckas jag nu få fram med bra hjälp från Laguna. Genom den tänkta triangel jag använde för att få fram Z kan jag även få fram X-värdet, som går lodrätt ner från cirkelns medelpunkt. Kateter X och kateter Z möts lodrätt under medelpunkten med 90 graders vinkel.
Cos 35 grader = X / 19
X = Cos 35 grader * 19
X = Ca 15,564
Till vänster på ritningen ser man att diametern är 80 mm. Radieprogrammering ska vi ha här och radien är 40 mm upp till cirkelns medelpunkt där man kan läsa R19. Då kan man dra ifrån 15,564 från 40 och få sökta punktens position i höjdled.
X (höjd) på ritningen för punkt 4 = 40 - 15,564 = Ca 24,44.
Tack Laguna!


