2
svar
57
visningar
Liten nattkluring #2
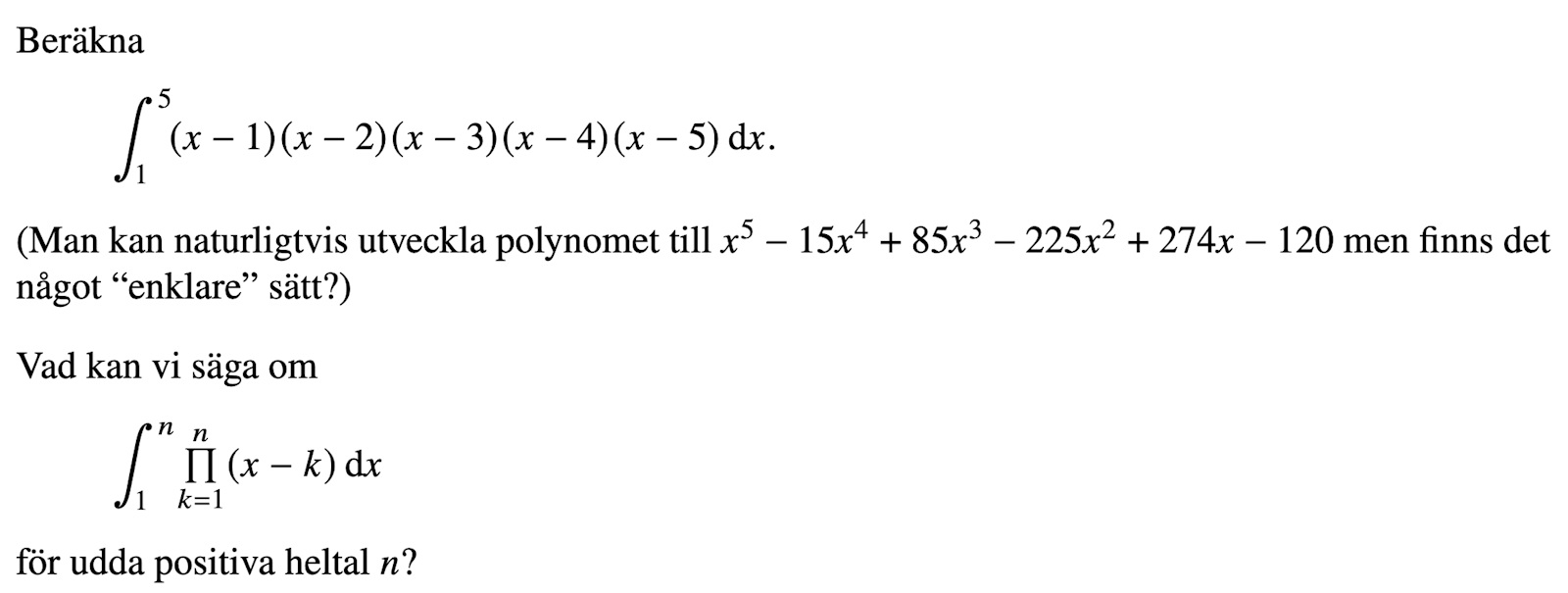
Visa spoiler
Låt för positivt heltal och substituera . Då får vi att
Vi ser att integralen är över ett symmetriskt intervall runt , alltså över , ()
och integrandet är funktionen . Denna funktion är udda eftersom varje faktor på formen kan paras ihop med faktorn för att bilda en jämn funktion, . Detta gäller för alla och den enda som "saknar ett par" är -faktorn.
Vi kan då skriva som en produkt av jämna funktioner tillsammans med en udda funktion, därmed är udda och då integreras på ett symmetriskt intervall blir integralens värde 0.
Mycket vackert AlexMu!

