Liten nattkluring #3
När ändå "flitens lampa lyser"...

Visa spoiler
Supersnyggt!
Nämnaren är misstänksamt nära . Vi får
Notera att har samma nämnare och då är
Låt
Då denna summa är ändlig kan vi "byta riktning" och summera åt andra hållet. Vi gör detta genom att substituera . Då får vi
Detta ger då att
PS: För slutet blev jag påmind om den kända historien om en lösning till (sagt att Gauss kom på detta som mycket ung?) där man dubblerar summan och byter riktning för att summera ihop alla termer till . Roligt sätt att tänka!
AlexMu skrev:Visa spoiler
Supersnyggt!
Nämnaren är misstänksamt nära . Vi får
Notera att har samma nämnare och då är
Låt
Då denna summa är ändlig kan vi "byta riktning" och summera åt andra hållet. Vi gör detta genom att substituera . Då får vi
Detta ger då att
Så vackert. Precis min observation också även om jag skrev
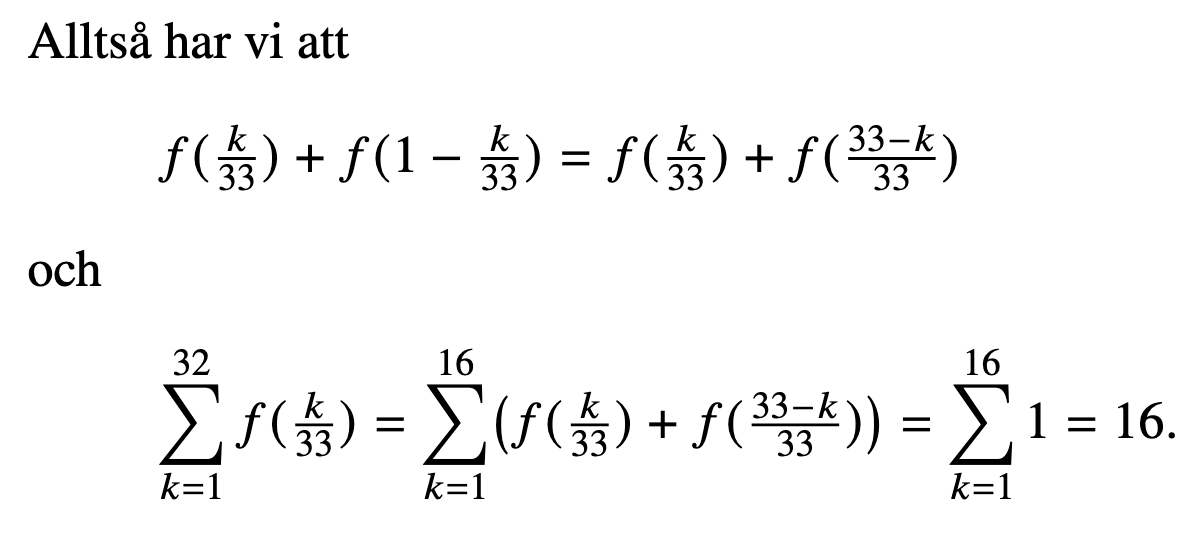
Ja, jag tycker om att addera ihop olika varianter av samma summa/integral och se någon snygg förenkling ske! Om jag ser något sådant brukar jag alltid göra det.

