Liten nattkluring #5

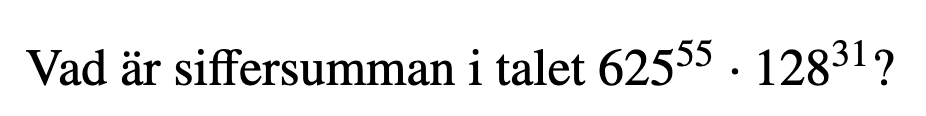
Man kan börja med 

$625 = 5^4$ och $128=2^7$

och då blir

$625^{55} \cdot 128^{31} = 5^{4 \cdot 55} \cdot 2^{7 \cdot 31} = 5^{220} \cdot 2^{217}$

Sedan märker man att $5 \cdot 2 = 10$, så det blir massa nollor i slutet av talet och de kommer inte att bidra till siffersumman.

$5^{220} \cdot 2^{217} = 5^3 \cdot (5 \cdot 2)^{217}=125 \cdot 10^{217}$.

Siffersumman blir $1+2+5=8$