Ljudvågor

De där två formlerna är användbara. Du behöver fundera på vad A är när det står ”åt alla håll” i uppgiften. Ersätt A med ett uttryck som innehåller avståndet r så tror jag du kommer vidare. 

Jo, A blir A=4•pi•r²

men jag har lite svårt att tolka uppgiften

ska jag först beräkna med värdet  r=1 m

och sedan r=10 m

eftersom jag behöver ljudintensiteten?

Absolut!

Det är dock enklare än så. Man behöver inte räkna ut intensiteten. 

Du har ett okänt I_O. Låt oss säga att det är =1. Om r ökar med en faktor x10 i I=P/A, vad händer då med I? 

Det ger dig en ny intensitet I för r=10.

Hur stor förändring i ljudnivå (dB) motsvarar detta förhållande i ljudintensitet? 

Om A blir större så kommer I (ljudintensiteten) att minska.

Jag hänger inte riktigt med genvägen. I_O är inte L₀ (jämförelsekonstanten)?

är det relaterad till detta :https://sv.wikipedia.org/wiki/Inversa_kvadratlagen

Ungefär så här menade jag.

Vi kan absolut räkna via faktiska ljudintensiteter:

$L_{1m}=10\times \log \left(\frac{I_{1m}}{I_0}\right)$

Vi har att L_1m=77 dB och I₀ är 10^-12 W/m² (hörbarhetsgränsen).

$$\begin{gathered} 77=10\times \log \left(\frac{I_{1m}}{{10}^{-12}}\right) \\ {I}_{1m}\approx 5,0\times {10}^{-5} \mathrm{W}/{\mathrm{m}}^2 \end{gathered}$$

Det var precis vad du fick.

Nu kan vi nyttja att $I\propto \frac{1}{r^2}$.

Det betyder att om r ökar med en faktor x10, så minskar I med en faktor x100:

$L_{10m}=\raisebox{1ex}{$L_{1m}$}\!\left/ \!\raisebox{-1ex}{$100$}\right.$

Vi kan förstås räkna ut effekten genom att multiplicera med arean för en sfär med radien r=1 m och sedan dividera med arean för en sfär med radien r=10 m. Det blir precis samma sak.

Nu kan vi räkna ut den nya ljudnivån:

$$\begin{gathered} L_{10m}=10\times \log \left(\frac{I_{10m}}{I_0}\right) \\ {L}_{10m}=10\times \log \left(\frac{5,0\times {10}^{-7}}{{10}^{-12}}\right) \\ {L}_{10m}\approx 57 \mathrm{dB} \end{gathered}$$

Det kom du också fram till.

Men! Eftersom ljudnivå bara är förhållandet mellan en ljudintensitet och en referens, så behöver vi ju inte utgå ifrån hörbarhetsgränsen 10^-12 W/m².

Vi vet att på 10 m avstånd så är ljudintensiteten 1/100 av vad den är på 1 m. Vad än I₀ är så är vårt I en hundradel.

$$\begin{gathered} L_{10m}=10\times \log \left(\frac{{\displaystyle \raisebox{1ex}{$I_0$}\!\left/ \!\raisebox{-1ex}{$100$}\right.}}{I_0}\right)= \\ 10\times \log \left(\frac{1}{100}\right)=-20 \mathrm{dB} \end{gathered}$$

Det ger oss att L_10m är -20 dB. Minus?! Vad betyder det?

Jo, givet vår referensintensitet I₀ på 1 meters avstånd som vi inte räknat ut, är alltså ljudnivån på 10 meters avstånd -20 dB, alltså 20 dB lägre.

Eftersom uppgiften ger oss att den är 77 dB på 1 meter så är den 77-20=57 dB på 10 meter.

Det var bara det jag menade. Verkar det rimligt?

-så samma P används i beräkningen eftersom det är samma högtalare som avger samma totala effekt?

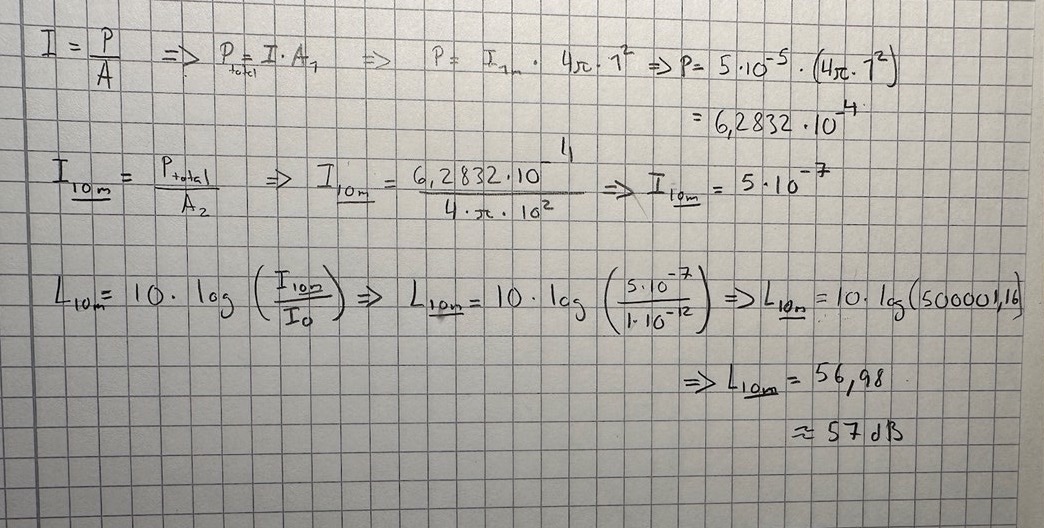
-i  denna del av beräkningen, så används hörbarhetsgränsen  2 gånger? :

Nej, jag borde kanske ha valt något annat. Där är I₀ intensiteten på 1 m håll där nivån är 77 dB. Vi behöver inte veta hur många W/m² den är. Allt vi behöver veta är att intensiteten i täljaren är en hundradel av den.