1
svar
41
visningar
Logaritmfunktions tangent
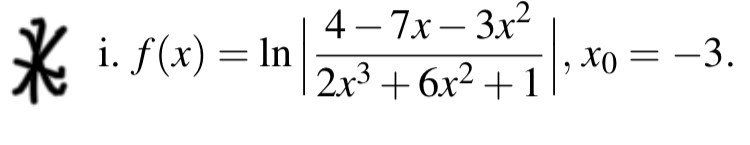
’Vad har jag gjort fel?
Första termen i f'(-3): -7-6x är 11, inte -11.
 Pluggakuten
Pluggakuten
En gratistjänst från Mattecentrum
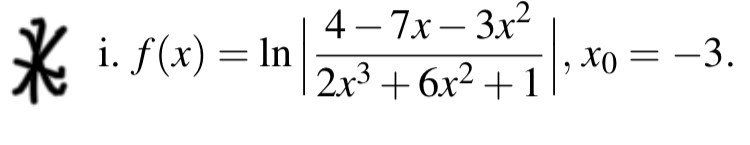
’Vad har jag gjort fel?
Första termen i f'(-3): -7-6x är 11, inte -11.