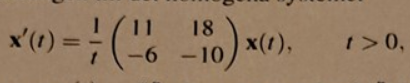Lös det inhomogena systemet

$r$ ska vara en konstant! Det ska inte finnas något $t$ i exponenten.

Gör ansats $\mathbf{x}\left(t\right) = t^r \begin{pmatrix} a \\ b\end{pmatrix} = \begin{pmatrix} a\,t^r \\ b \,t^r\end{pmatrix}$ och sätt in detta i den givna homogena ekvationen. $t^r$ kommer att förkortas, men sedan får du en ekvation  på formen "vektor = matris * vektor" utan några $t$ alls. Denna ekvation borde påminna dig om lösningsmetoden hur man söker egenvärden och egenvektorer till en matris.

LuMa07 skrev:

$r$ ska vara en konstant! Det ska inte finnas något $t$ i exponenten.

 

Gör ansats $\mathbf{x}\left(t\right) = t^r \begin{pmatrix} a \\ b\end{pmatrix} = \begin{pmatrix} a\,t^r \\ b \,t^r\end{pmatrix}$ och sätt in detta i den givna homogena ekvationen. $t^r$ kommer att förkortas, men sedan får du en ekvation  på formen "vektor = matris * vektor" utan några $t$ alls. Denna ekvation borde påminna dig om lösningsmetoden hur man söker egenvärden och egenvektorer till en matris.

Vad menar du med att t^r kommer förkortas? Jag förstår inte riktigt vad du menar med att sätta in detta i den homogena ekvationen.

Om $\mathbf{x}\left(t\right) = t^r \begin{pmatrix}a \\ b \end{pmatrix}$, så är $\mathbf{x}^\prime\left(t\right) = r\,t^{r-1} \begin{pmatrix}a \\ b \end{pmatrix}$ förutsatt att $r\ne 0$.

Detta stoppas in i den givna homogena ekvationen:

$r \,t^{r-1} \begin{pmatrix}a\\b\end{pmatrix} = \dfrac{1}{t} \begin{pmatrix}11&18\\-6&-10\end{pmatrix} t^r \begin{pmatrix}a\\b\end{pmatrix}  \iff$

$r \,t^{r-1} \begin{pmatrix}a\\b\end{pmatrix} = t^{r-1} \begin{pmatrix}11&18\\-6&-10\end{pmatrix} \begin{pmatrix}a\\b\end{pmatrix} \iff$

$r \, \begin{pmatrix}a\\b\end{pmatrix} = \begin{pmatrix}11&18\\-6&-10\end{pmatrix} \begin{pmatrix}a\\b\end{pmatrix}$

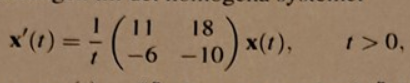
Det återstår att hitta vektorn $\begin{pmatrix}a\\b\end{pmatrix}$ och tillhörande talet $r$ så att ekvationen är uppfylld.

LuMa07 skrev:

Om $\mathbf{x}\left(t\right) = t^r \begin{pmatrix}a \\ b \end{pmatrix}$, så är $\mathbf{x}^\prime\left(t\right) = r\,t^{r-1} \begin{pmatrix}a \\ b \end{pmatrix}$ förutsatt att $r\ne 0$.

Detta stoppas in i den givna homogena ekvationen:

$r \,t^{r-1} \begin{pmatrix}a\\b\end{pmatrix} = \dfrac{1}{t} \begin{pmatrix}11&18\\-6&-10\end{pmatrix} t^r \begin{pmatrix}a\\b\end{pmatrix}  \iff$

$r \,t^{r-1} \begin{pmatrix}a\\b\end{pmatrix} = t^{r-1} \begin{pmatrix}11&18\\-6&-10\end{pmatrix} \begin{pmatrix}a\\b\end{pmatrix} \iff$

$r \, \begin{pmatrix}a\\b\end{pmatrix} = \begin{pmatrix}11&18\\-6&-10\end{pmatrix} \begin{pmatrix}a\\b\end{pmatrix}$

Det återstår att hitta vektorn $\begin{pmatrix}a\\b\end{pmatrix}$ och tillhörande talet $r$ så att ekvationen är uppfylld.

Ja ok. Då är jag med! r är alltså egenvärdet och (a b) är vektorn så det är samma likhet som lambdav =Av i linjär algebra.