Lös ekvation med en rot med realdelen 1
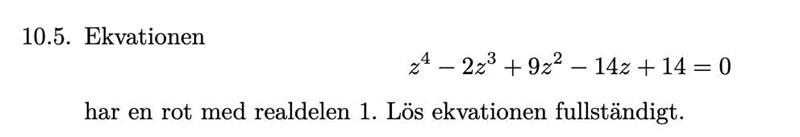
Mitt försök:
Fjärdepotensen borde ha en y2- och en y-term i sig också.
Ok, men om jag lägger till det som saknas från fjärde-potensen vilket är:
Hjälp tack!
Jag provade med en annan metod: Eftersom det ska finnas en rot 1+yi så är också 1-yi en rot. Det betyder att z2-2z+a är en faktor i polynomet, där a är nåt reellt tal. Med polynomdivision hittar man y och a.
Laguna skrev:Jag provade med en annan metod: Eftersom det ska finnas en rot 1+yi så är också 1-yi en rot. Det betyder att z2-2z+a är en faktor i polynomet, där a är nåt reellt tal. Med polynomdivision hittar man y och a.
Jag fick att en faktor i polynomet är:
'
Nej. Du har fått fel tecken på den första termen zyi och du har tappat bort termen 1.
Smaragdalena skrev:Nej. Du har fått fel tecken på den första termen zyi och du har tappat bort termen 1.
Oj, det blev fel. Men var kommer a in i bilden som laguna påpekade?
a införde jag bara för att slippa tänka ut och skriva vad konstanttermen skulle vara medan jag polynomdividerade. Du kan strunta i a.
Laguna skrev:a införde jag bara för att slippa tänka ut och skriva vad konstanttermen skulle vara medan jag polynomdividerade. Du kan strunta i a.
Jaha ok, då vet jag



