Lös ekvationen (Matematik/Matte 2/Linjära ekvationssystem)

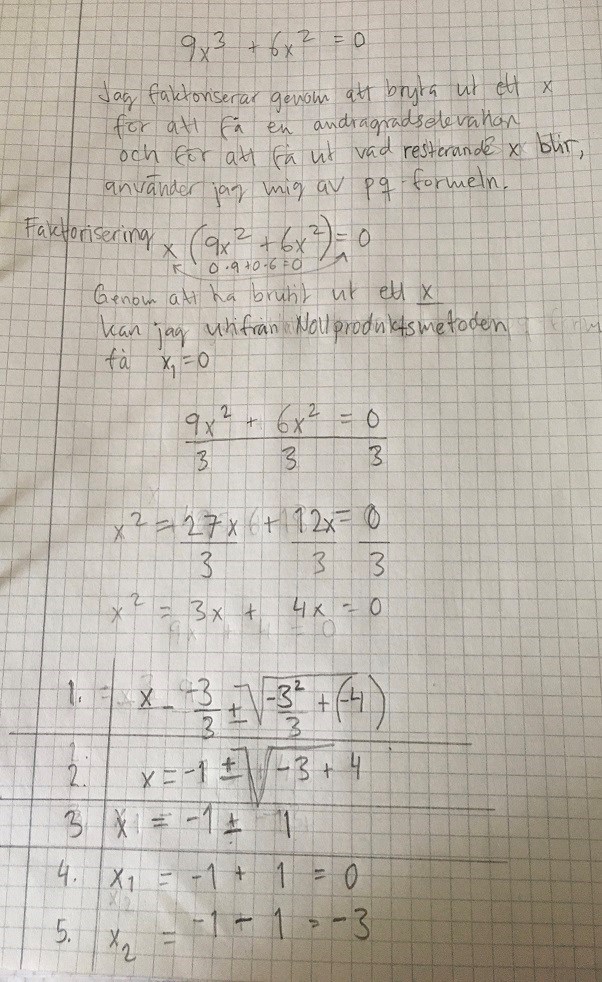
Nej det stämmer inte.

Om du bryter ut $x$ så blir det $(9x^2+6x)$ kvar innanför parentesena, inte det du skriver. Sedan förstår jag inte vad du gör, men det blir iallafall inte rätt.

Men det är enklare att bryta ut $3x^2$ istället.

Det blir fel när du bryter ut x, tyvärr. Bryt ut x, så att du får $x(9x^2+6x)$ , inte $6x^2$ . :) Det fina är nu att du nu kan bryta ut ännu en faktor x. Vad får du då? :)

Dags för paus men återkommer med en ny uträkning senare ikväll.

Smutstvätt skrev:
Det blir fel när du bryter ut x, tyvärr. Bryt ut x, så att du får $x(9x^2+6x)$ , inte $6x^2$ . :) Det fina är nu att du nu kan bryta ut ännu en faktor x. Vad får du då? :)

Jag har nu brutit ut båda x och fått ekvationen till x³ (9x+6x)=0

Eller skulle jag bara bryta ut totalt 2 x så jag får: x² (9x²+6x)=0

Har jag missförstått dig?

Om du multiplicerar ihop de uttryck som du har fått fram, skall du få tillbaka den ekvation du hade från början. Om du inte får det, har du gjort fel.

Vi kontrollerar dina förslag på faktoriseringar genom att multiplicera ihop dem:

$x^3(9x+6x)=x^3\cdot9x+x^3\cdot6x=9x^4+6x^4$ . Det stämmer inte.

$x^2(9x^2+6x)=9x^4+6x^3$ . Det stämmer inte.

------

Är du med på att $9x^3$ kan delas upp i de två faktorerna $x^2$ och $9x$ ?

Är du med på att $6x^2$ kan delas upp i de två faktorerna $x^2$ och $6$ ?

Är du med på att $x^2$ är en gemensam faktor i de båda termerna och att det som "blir kvar" är $9x$ respektive $6$ ?

Är du med på att det då gäller att $9x^3+6x^2=x^2(9x+6)$ ?

Jag tror jag är med. Jag återkommer och tack för att ni finns.

migge83 skrev:
Jag tror jag är med. Jag återkommer och tack för att ni finns.

Vad bra. Jag korrigerade ett par småfel i mitt förra svar.

Kom ihåg att alltid alltid kontrollera dina faktoriseringar genom att multiplicera ihop och se om du då får tillbaka ursprungsuttrycket.

Jag har verkligen kört fast. Jag kommer inte längre än faktorisera 9x³+6x² så att det blir

x²(9x+6²) och/eller x³(9x+6x).

Glömmer jag fortfarande nåt? Känner mig så förvirrad. Det hjälper inte att pausa. Jag läser era svar flera gånger och jag tittar på olika videon men det är som att inget vill fastna. Jag har tydligen svårt att förstå.

Ta det lugnt, vi löser det här. Vi börjar med att kontrollera dina båda förslag.

Förslag 1: Kan $x^2(9x+6^2)$ vara en korrekt faktorisering av $9x^3+6x^2$ ? Multiplicera ihop ditt förslag, vad får du då fram?

Förslag 2: Kan $x^3(9x+6x)$ vara en korrekt faktorisering av $$9x^3+6x^2)? Multiplicera ihop ditt flrslag, vad får du då fram?

Förstår du vad vi menar när vi säger att du ska kontrollera om din faktorisering är rätt?

Förstår du hur du ska göra det?

Det går väl under Konjugatregeln och kvadreringsreglerna men i detta fall gäller väl endast konjugatregeln?

migge83 skrev:
Det går väl under Konjugatregeln och kvadreringsreglerna men i detta fall gäller väl endast konjugatregeln?

Nej här behöver du varken kvadreringsreglerna eller konjugatregeln. Det du behöver är att veta hur man multiplicerar in en faktor i parenteser.

Vet du hur man gör det?

Dvs vet du vad man får om man multiplicerar ihop till exempel $a(b+c)$ ?

ab+ac men jag får problem att göra det med ekvationen som går under denna tråd. Jag är osäker på om jag ska multiplicera x med samtliga tecken i parantesen.

Mitt problem är att det blir som ett helt annat språk eller hur jag nu ska förklara.

migge83 skrev:
ab+ac men jag får problem att göra det med ekvationen som går under denna tråd. Jag är osäker på om jag ska multiplicera x med samtliga tecken i parantesen.
Mitt problem är att det blir som ett helt annat språk eller hur jag nu ska förklara.

Om du skall multiplicera ihop x²(9x+6) skalll du multiplicera x² dels med 9x, dels med 6.

Smaragdalena skrev:
migge83 skrev:
ab+ac men jag får problem att göra det med ekvationen som går under denna tråd. Jag är osäker på om jag ska multiplicera x med samtliga tecken i parantesen.
Mitt problem är att det blir som ett helt annat språk eller hur jag nu ska förklara.
Om du skall multiplicera ihop x²(9x+6) skalll du multiplicera x² dels med 9x, dels med 6.

Det får jag till 9x²+6x

Nej. Vad är x^2.x? Vad är x^2.6? Vad är x^2.9x?

Smaragdalena skrev:
Nej. Vad är x^2.x? Vad är x^2.6? Vad är x^2.9x?

x^2*x=2x²
x²*6=6x²
x²*9x=9³

Det är väl det här som går under Distributiva lagen och Utvidgade distributiva lagen?

migge83 skrev:
Smaragdalena skrev:
Nej. Vad är x^2.x? Vad är x^2.6? Vad är x^2.9x?
x^2*x=2x²
x²*6=6x²
x²*9x=9³

Det är väl det här som går under Distributiva lagen och Utvidgade distributiva lagen?

Nej, inget distributivt här. Distributiva lagen handlar om att multiplikation distribueras, alltså fördelas, över alla termerna i ett additionsuttryck a(b+c) = ab+ac. Och också att potens distribueras över multiplikation (ab)^c = a^cb^c, är det det du tänker på?

Av dina svar är bara 6x² rätt.

Laguna skrev:
migge83 skrev:
Smaragdalena skrev:
Nej. Vad är x^2.x? Vad är x^2.6? Vad är x^2.9x?
x^2*x=2x²
x²*6=6x²
x²*9x=9³

Det är väl det här som går under Distributiva lagen och Utvidgade distributiva lagen?
Nej, inget distributivt här. Distributiva lagen handlar om att multiplikation distribueras, alltså fördelas, över alla termerna i ett additionsuttryck a(b+c) = ab+ac. Och också att potens distribueras över multiplikation (ab)^c = a^cb^c, är det det du tänker på?
Av dina svar är bara 6x² rätt.

Hmm ja det här verkar hopplöst. Jag tycks blanda ihop allt. Det tycks vara så att jag blandar ihop antalet x med ^, att jag fördelar dem fel. Är följande korrekt uppfattat------> 9³x+6² = x³(9x+6+2) eller x²⁺³(9+6)?

Jag kom just fram till att det är Potenslagarna jag inte har koll på.

Det kan vara bra om du går igenom allt som har med algebra att göra från sjuan och framåt. (Om sjuan etc. går som en dans så har du inte förlorat nån tid på att repetera.) Du fastnar förmodligen nånstans, och då kan vi försöka reda ut saken.

Laguna skrev:
Det kan vara bra om du går igenom allt som har med algebra att göra från sjuan och framåt. (Om sjuan etc. går som en dans så har du inte förlorat nån tid på att repetera.) Du fastnar förmodligen nånstans, och då kan vi försöka reda ut saken.

Ja så får det bli. Jag har redan accepterat att jag blir underkänd. Jag visste att jag inte var bättre än så här men vad kan man begära om man inte läst på 17 år och redan var dålig.

Testar igen;

x2*x=x³
x²*6=6x²
x²*9x=9x³

Har jag rätt på samtliga?

Ja om du menar $x^2x$ på den första så är allt rätt.

Det kan underlätta att tänka att "upphöjt till" är en upprepad multiplikation "med sig själv".

Exempel:

$x^2=x\cdot x$

$x^3=x\cdot x\cdot x$

$x^4=x\cdot x\cdot x\cdot x$

och så vidare.

Jag tror att jag rätt ute. Jag har försökt att bryta ut 2 x och använt mig av Nollproduktsmetoden.

Missar jag fortfarande nåt?

Om jag vill verifiera så kör jag väl bara pq-formeln?

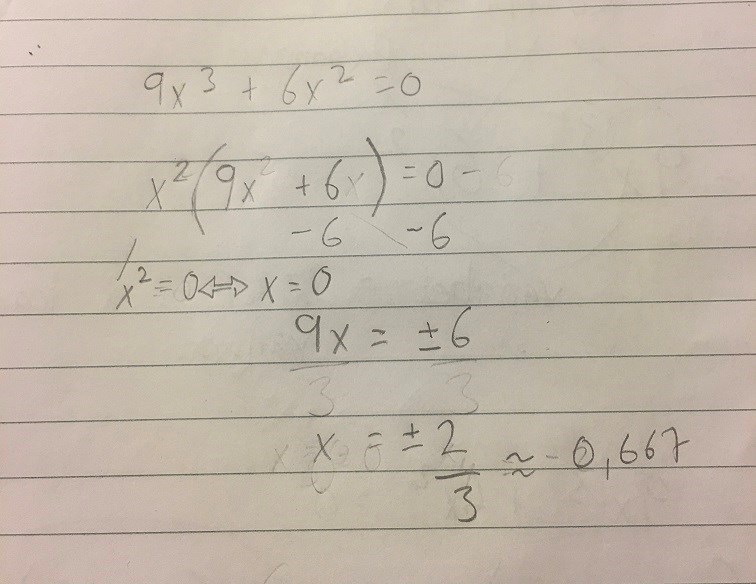
Om du vill verifiera är det bäst att sätta in dina framräknade värden i den ursprungliga ekvationen.

9x+6 = 0 har bara en lösning. Om 9x = 6 så är summan 12, inte 0.

Tänkte på det här med pq;

Om man faktoriserar så 9x³+6x² blir;

3x² (3x+2)=0,

Behöver man visa det med pq-formel också då man endast genom Nollproduktmetoden kan identifiera att samtliga 3 (x)=0?

I uppgiften ombeds man endast att lösa ekvationen.

pq-formeln gäller för första- och andragradsekvationer. Du har just löst en tredjegradsekvation

Om du vill kontrollera ditt svar skulle jag rekommendera att du bara sätter in dina lösningar. $x_{1,2}=0$ ger trivialt 0.

$x=-2/3$ ger (för parentesen)

$(3x+2)=(3(- \frac{2}{3})+2)=-2+2=0$

Alltså är lösningarna korrekta.

Edit: strök över ett ord som ramlade med i hastigheten!

Nej pq-formeln funkar endast för andragradsekvationer, inte för förstagradsekvationer.

Yngve skrev:
Nej pq-formeln funkar endast för andragradsekvationer, inte för förstagradsekvationer.

Ja, det är ju förstås korrekt :)

Vi ska iaf inte försöka kontrollera en tredjegradsekvation med pq-formeln.