lös ekvationen mha grafen

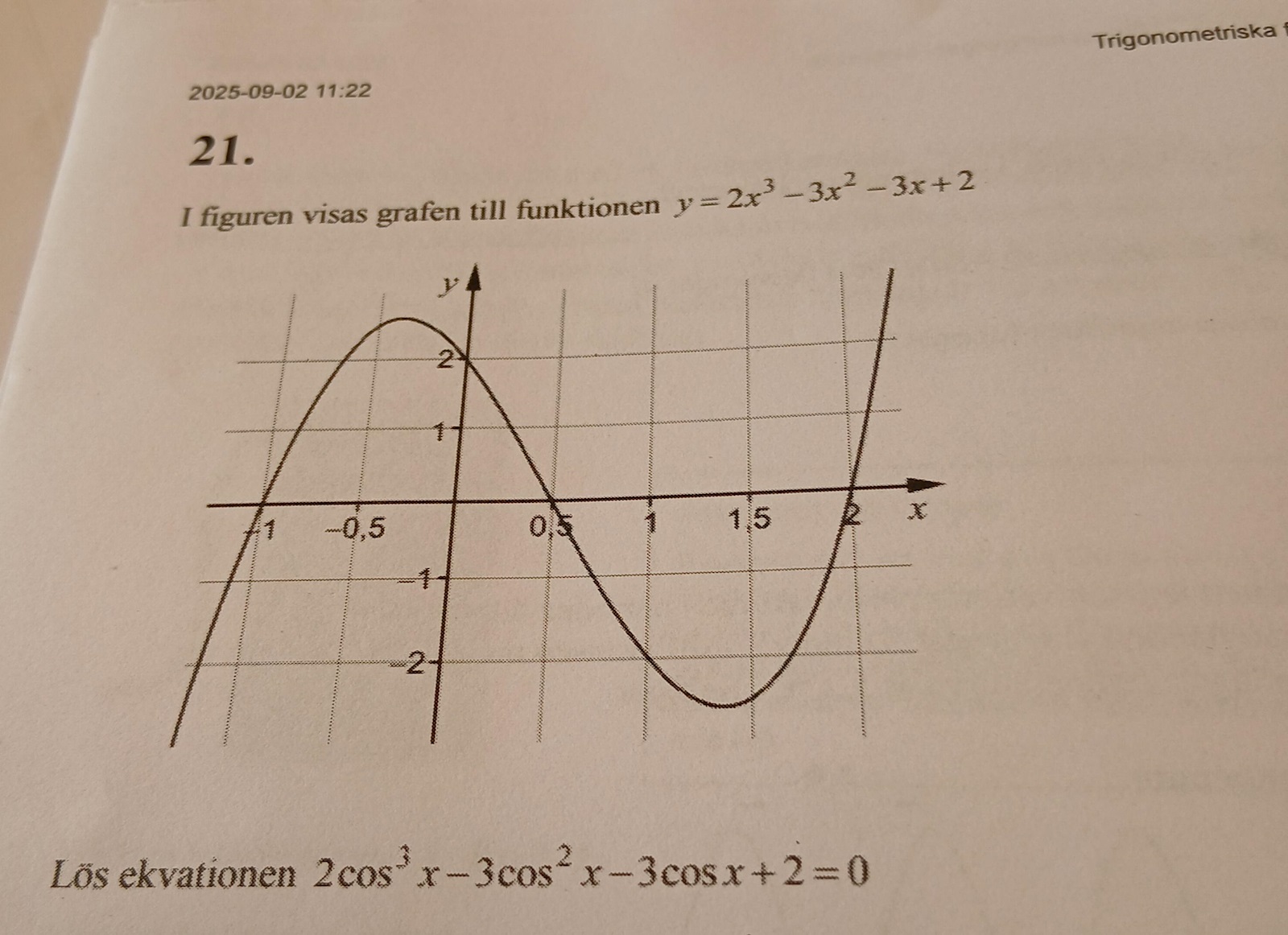
I grafen hittar du lösningarna till 2x³ - 3x² - 3x + 2 = 0

I samma graf hittar du såklart lösningarna till 2t³ - 3t² - 3t + 2 = 0. Vilket namn den okända variabeln har kan ju kvitta.

Vad måste alltså cos(x) vara, för att 2(cos(x))³ - 3(cos(x))² - 3cos(x) + 2 = 0

Bubo skrev:

I grafen hittar du lösningarna till 2x³ - 3x² - 3x + 2 = 0

I samma graf hittar du såklart lösningarna till 2t³ - 3t² - 3t + 2 = 0. Vilket namn den okända variabeln har kan ju kvitta.

Vad måste alltså cos(x) vara, för att 2(cos(x))³ - 3(cos(x))² - 3cos(x) + 2 = 0

Jag vet inte vilka samband jag kan nyttja. Är det möjligtvis när $\cos \left(x\right)=0 ?$

Nej, 2*0³ - 3*0² - 3*0 + 2 blir inte noll.

Samma fråga igen:

Vad måste  snfp(g) vara, för att 2(snfp(g))³ - 3(snfp(g))² - 3snfp(g) + 2 = 0

det är ju en tredjegradsekvation. Jag antar väl att jag ska lösa den digitalt för formeln är väldigt avancerad för min (nuvarande) nivå.

Du vet ju vad x ska vara för att 2x³ - 3x² - 3x + 2 = 0

...och namnet på en variabel spelar ingen roll.

Bubo skrev:

Du vet ju vad x ska vara för att 2x³ - 3x² - 3x + 2 = 0

...och namnet på en variabel spelar ingen roll.

Justdet jag kan kan kolla på grafen och se när den skär x-axeln.

Arup skrev:

Bubo skrev:

Du vet ju vad x ska vara för att 2x³ - 3x² - 3x + 2 = 0

...och namnet på en variabel spelar ingen roll.

Justdet jag kan kan kolla på grafen och se när den skär x-axeln.

Precis!

$\cos x=x_i$ där $i=1,2,3$