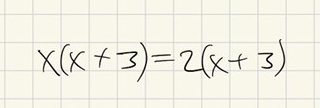Lös ekvationen (Np 3b/3c ht13) (Matematik/Matte 3/Algebraiska uttryck)

Vad händer om du sätter in x = 3 i ursprungsekvationen?

Tures råd är alldeles utmärkt! Det är väldigt bra att ta som vana att sätta in de lösningar man får i ursprungsekvationen, för att kontrollera att man räknat rätt.

Det du har hittat är en falsk rot. De får man passa sig för, exempelvis när man förkortar/dividerar med ett uttryck som kan bli =0. I ditt fall förkortar du med (x-3) som blir noll då x=3. Division med noll är ju inte OK, så det var inte giltigt att göra (även om man inte ser det när man löser). Där kommer efterkontrollen in!

Ett annat exempel är kvadratrötter och potenser:

$\sqrt{x + 6} = x$

Vi kvadrerar VL och HL:

$x + 6 = x^{2}$

Sedan löser vi:

$x^{2} - x - 6 = 0 (x - 3) (x + 2) = 0 x_{1} = 3 x_{2} = - 2$

Men! Kvadratrötter spottar ju bara ur sig positiva tal, så x=-2 kan inte vara en lösning:

$\sqrt{- 2 + 6} = \sqrt{4} \neq - 2$

Alltså är x₂=-2 en falsk rot som vi introducerat när vi löste ekvationen.

sictransit skrev:
$x^{2} - x - 6 = 0 (x - 3) (x + 2) = 0 x_{1} = 3 x_{2} = - 2$

Lite OT. Hur såg du detta? (Alltså från första till andra raden)

tror jag varit inne på det några gånger här: https://www.pluggakuten.se/trad/los-ekvationerna-varfor-eliminerar-man-en-rot/

här: https://www.pluggakuten.se/trad/los-ekvationerna-falska-rotter/

och ngn till gång. Fick det bra förklarat Luma förut.

hmm, jag försöker lösa detta igen då utan att introducera en rot..

maratmatorkin skrev:
sictransit skrev:
$x^{2} - x - 6 = 0 (x - 3) (x + 2) = 0 x_{1} = 3 x_{2} = - 2$

Lite OT. Hur såg du detta? (Alltså från första till andra raden)

tror jag varit inne på det några gånger här: https://www.pluggakuten.se/trad/los-ekvationerna-varfor-eliminerar-man-en-rot/

här: https://www.pluggakuten.se/trad/los-ekvationerna-falska-rotter/

och ngn till gång. Fick det bra förklarat Luma förut.

hmm, jag försöker lösa detta igen då utan att introducera en rot..

OK. Det var kanske lite väl kortfattat, men ekvationen går förstås även att lösa med pq-formeln.

Generellt gäller att om koefficienten framför x² är =1, så kan man faktorisera som jag gjorde genom att hitta två tal som adderar till p och multiplicerar till q. Vet inte när i matten det dyker upp, men det är ju lätt att konstatera att det stämmer.

Men hur löser jag den om jag inte får multiplicera så att jag får samma nämnare?

Eller är det snarare så att den inte är definierad för 3 som i exemplet i boken:

maratmatorkin skrev:
Men hur löser jag den om jag inte får multiplicera så att jag får samma nämnare?

Börja med att titta på ursprungsekvationen, då konstaterar man snabbt att

x = 0 och x = 3 är otillåtna lösningar eftersom en eller flera nämnare blir 0 för de värdena.

Sen löser du ekvationen på vanligt sätt. Om någon av lösningarna blir 0 eller 3 så är det en falsk rot som ska förkastas. Övriga eventuella lösningar är ok.

Rent generellt när det gäller ekvationslösning, ta för vana att kontrollera ditt svar genom att sätta in lösningarna i ursprungsekvationen och säkerställ att HL = VL,
och var uppmärksam när du delar med faktorer som för vissa värden på x kan bli 0.

Ture skrev:
maratmatorkin skrev:
Men hur löser jag den om jag inte får multiplicera så att jag får samma nämnare?

Börja med att titta på ursprungsekvationen, då konstaterar man snabbt att

x = 0 och x = 3 är otillåtna lösningar eftersom en eller flera nämnare blir 0 för de värdena.

Sen löser du ekvationen på vanligt sätt. Om någon av lösningarna blir 0 eller 3 så är det en falsk rot som ska förkastas. Övriga eventuella lösningar är ok.

Rent generellt när det gäller ekvationslösning, ta för vana att kontrollera ditt svar genom att sätta in lösningarna i ursprungsekvationen och säkerställ att HL = VL,
och var uppmärksam när du delar med faktorer som för vissa värden på x kan bli 0.

Tack!🙏

Typ som här då? Detta var nästa uppgift och här skrev jag direkt ut vad det inte fick bli så att säga. Fick rätt svar även om det tog mig 30 min och mycket huvudbry.. behövde ta 5 min rast å sen slog det i blått mig..

Eller denna.. börjar haja grejen. Tack!

I din sista uppgift finns det en fälla, som du inte gick i!

När du kommit hit:

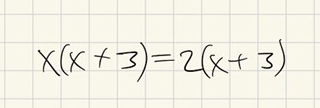
Är det frestande att dela bägge led med (x+3) och därmed få svaret x = 2, vilket ju i och för sig är en giltig rot, men då tappar man bort x = -3

Det är en följd av samma fenomen, man delar med ngt som kan vara = 0

Du utvecklade istället bägge led och fick då med bägge lösningarna.

Ture skrev:
I din sista uppgift finns det en fälla, som du inte gick i!

När du kommit hit:

Är det frestande att dela bägge led med (x+3) och därmed få svaret x = 2, vilket ju i och för sig är en giltig rot, men då tappar man bort x = -3

Det är en följd av samma fenomen, man delar med ngt som kan vara = 0

Du utvecklade istället bägge led och fick då med bägge lösningarna.

Just det! Ser det nu också. Bra exempel.