Lös ekvationen sin 3x = sin x

Det behöver du inte. Om två sinusfunktioner ska ge samma värde måste deras argument vara lika. Det är grundidén. Sedan behöver man bara ta hänsyn till perioden så är man hemma!🤪

Gillar du trigonometriska samband, kan du ta det översta (nedan) och fortsätta där du är. Det blir en rätt så prydlig lösning. 

En regel:

sin u = sin v

<==>

u = v + n•360 ELLER u=180-v +n•360

sictransit skrev:

Gillar du trigonometriska samband, kan du ta det översta (nedan) och fortsätta där du är. Det blir en rätt så prydlig lösning. 

Jag försöker lista ut vad det är som händer här, Men ha fastnat. Hur får du på HL att det blir det?

Det liknar nästan dubbla vinkel med sin2v=2sin v cos v. Var får man 2 ifrån och divisionen?

M (a) * x skrev:

sictransit skrev:

Gillar du trigonometriska samband, kan du ta det översta (nedan) och fortsätta där du är. Det blir en rätt så prydlig lösning. 

Jag försöker lista ut vad det är som händer här, Men ha fastnat. Hur får du på HL att det blir det?

Det liknar nästan dubbla vinkel med sin2v=2sin v cos v. Var får man 2 ifrån och divisionen?

Jag har inte härlett det. Slog upp det i en lista över trigonometriska samband. Det såg användbart ut för din uppgift. 

Det kan vara en listig metod. Men det är nog bättre att lära sig de standardmetoder som finns för trigonometriska ekvationer till en början.

Men vilken metod ska man använda helst.

Är det bättre att flytta över så det blir minus?

Jag skulle anvönda det generella sambandet som Tomten beskriver i svar #4 och därigenom få fram följande två ekvationer: 

• 3x = x + n*360°
• 3x = 180°-x+n*360°

Jag löser sedan ut x för att få fram alla lösningar.

Yngve skrev:

Jag skulle anvönda det generella sambandet som Tomten beskriver i svar #4 och därigenom få fram följande två ekvationer: 

• 3x = x + n*360°
• 3x = 180°-x+n*360°

Jag löser sedan ut x för att få fram alla lösningar.

Ah, jag gjort precis det. Alltså har man sin x = sin x kan man skriva x = x +n*2*pi (första fallet)

M (a) * x skrev:

Ah, jag gjort precis det. Alltså har man sin x = sin x kan man skriva x = x +n*2*pi (första fallet)

Nja, ekvationen sin(x) = sin(x) har oändligt många lösningar, nämligen alla möjliga värden på x.

Menar du något annat?

Yngve skrev:

M (a) * x skrev:

Ah, jag gjort precis det. Alltså har man sin x = sin x kan man skriva x = x +n*2*pi (första fallet)

Nja, ekvationen sin(x) = sin(x) har oändligt många lösningar, nämligen alla möjliga värden på x.

Menar du något annat?

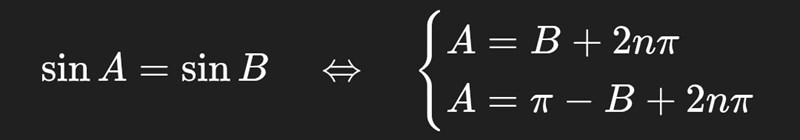
Ja, det stämmer.

Tomten skrev samma samband i svar #4, fast med vinklarna i grader istället.

Det kan oxå vara bra att använda enhetscirkeln för att visa för sig själv varför man lägger på en period och varför man får två fall. Med detta kanske du kan lista ut hur liknande samband borde se ut för cos(u)=cos(v).