lös ekvationerna

Hej, Skulle behöva hjälp med den här. Har kört fast och förstår inte riktigt.
a)
v=3x-pi/2
cos v=31/2/ 2
v=?
x=?
b)
v=2x-pi/4
sin v=1/21/2
v=?
x=?
jag fattar inte..
blir v i a) = ?
blir v i b) = ?
Hej.
Vi tar en sak i taget.
Ekvationen har lösningarna .
Vi kan dela upp detta i två grupper:
I vår ekvation är , vilket ger dig de två lösningsmängderna
Lös ut ur de båda ekvationerna och välj det/de värden på heltalet som gör att hamnar i det önskade intervallet.
Visa dina försök och fråga om allt som är oklart.
jag fattar inte :( det är så svårt alltihop.. så den här uppgiften löser man med formeln ekvationen tanv=k
v=arctank+n*pi (där n är ett godtyckligt tal)
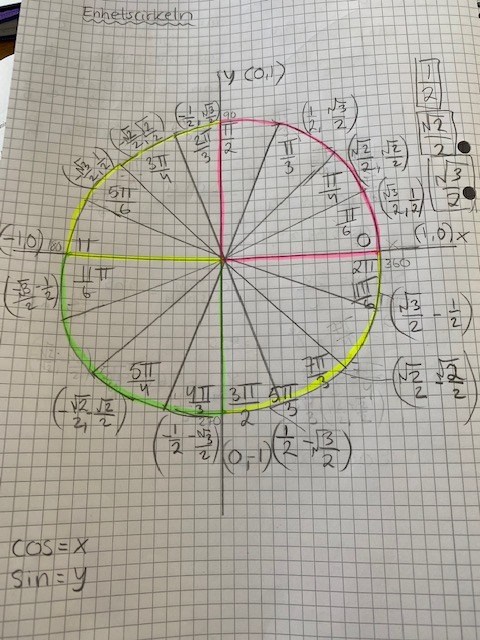
ursäkta min fula bild men vill verkligen förstå den här enhetscirkeln.
Jag förstår inte vad tan(v) har med uppgiften att göra.
Vi gör en förenkling och kallar tillfälligt för .
Då lyder ekvationen .
Eftersom alla punkter på enhetscirkeln kan skrivas i koordinatforn som så är ekvationens lösningar alla de värden på vinkeln för vilka "den första" koordinaten på enhetscirkeln har värdet .
Du kan direkt ur din fina enhetscirkel utläsa att två lösningar är och . Jag har markerat dessa i figuren.
Eftersom cosinus är en periodisk funktion med oerioden så måste vi lägga till perioden på våra lösningar och vi får då
och
Hänger du med så långt?
ja nu ser jag. Hänger med på det. Men hänger inte med på hur jag löser dem.
OK bra. Vad mer exakt är det du inte hänger med på?
hur jag löser ut x.
Det är inget magiskt, bara vanlig ekvationslösning. Vi tar en i taget:
Eftersom så får vi
Addera till båda sidor:
Förenkla HL:
Dividera båda sidor med 3:
Hängde du med?
Kan du göra samma sak med den andra ekvationen?
hängde med på allt förutom de två sista stegen... hur blir det ?
är det att vi ska få MGN där och multiplicerar ihop det så det blir 8pi/24 /8 = 1pi/3? men då hänger jag inte med på att det blir 2pi/3
blir inte den andra ekvationen samma?
Joh_Sara skrev:hängde med på allt förutom de två sista stegen... hur blir det ?
Högerledet:
Förläng andra termen med 3:
Sätt de båda första termerna på gemensamt bråkstreck:
Förenkla:
Förkorta första termen med 2:
hmmm känner mig lite vilse här: men vi hade x=
Nej titta igenom detta svar igen.
jag får inte riktigt ihop detta :(
Vilket/vilka av följande steg är det du fastnar på?
- Ekvationen är
- För att förenkla ekvationen inför vi tillfälligt variabeln
- Ekvationen kan då skrivas
- Den ekvationen har de två lösningsmängderna och
- Vi tittar nu endast på den första lösningsmängden. Den andra kan senare hanteras på motsvarande sätt.
- Eftersom så kan den första lösningsmängden skrivas
- Om vi adderar till bägge sidor får vi
- Vi förlänger andra termen i högerledet med 3 och får då
- De båda första termerna i högerledet har nu samma nämnare och vi kan därför sätta dem på gemensamt bråkstreck.
- Ekvationen blir då
- Efter förenkling blir ekvationen
- Vi förkortar första termen i högerledet med 2 och ekvationen blir då
- Nu dividerar vi bägge sidor med 3 och får då
okej jag tror jag är med. Har testräknat och det känns ok.
i ekvation 2 blir det då:
Stämmer det?
Ja det stämmer. Bra!
Nästa steg är att se vilken/vilka av alla dessa lösningar som hamnar inom det tillåtna intervalmet.
Pröva med några olika värden på konstanten .
Vusa dina resultat.
har testat att räkna uppgift b)
asså jag fattar inte riktigt men förösker såhär-
jag fattar att jag ska sätta in värden på n men förstår inte ritkgit hur jag sak räkna.
Joh_Sara skrev:asså jag fattar inte riktigt men förösker såhär-
jag fattar att jag ska sätta in värden på n men förstår inte ritkgit hur jag sak räkna.
Du behöver inte använda 27 som nämnare, 9 går bra. Men det är rätt i alla fall, så frågan är om är mindre än .
okej, nej det blir större än 3,14. Det blir 8,37. Hur ska mjag tänka och vad blir svaret? blir förvirrad.. Jag natar att jag ska ta reda på alla värden för n där svaret blir större än 0 men mindre än pi. ??
Du ska hitta alla värden på som ligger i intervallet .
Vi börjar med första lösningsmängden, dvs .
- Om får vi då . Det är utanför intervallet.
- Om får vi då . Det är inuti intervallet.
- Om får vi då . Det är inuti intervallet.
- Om får vi då . Det är utanför intervallet.
======
Nu tar vi den andra lösningsmängden, dvs .
- Om får vi då . Det är utanför intervallet.
- Om får vi då . Det är inuti intervallet.
- Om får vi då . Det är inuti intervallet.
- Om får vi då . Det är utanför intervallet.
========
Om vi räknar ihop det så hittar vi 4 lösningar inom intervallet, nämligen , , , .
Visa hur du räknade när du fick fram att är större än . Du multiplicerar ju med ett tal som är lite mindre än 1.
okej tack!
så i uppgift b) blir det såhär då;
sen blir jag lite osäker om jag räknat uppgift b rätt. Den finns lite längre upp i denna tråd om du skulle vilja kika på den?
för nästa lösningsmängd är x=0+n*2/2
Behöver inte bli så krångligt. Kan vara lättare att skissa cos och sin i ett diagram. Då ser man att i intervallet
har cos bara värdet för argumentet . D v s som ger
Sin däremot har värdet för både argumentet och , så man får ekvationerna
som ger och
som ger
Joh_Sara skrev:har testat att räkna uppgift b)
Nej det här stämmer inte.
Du blandar nog ihop lösningarna till cosinus- och sinusekvationer.
Ekvationen har lösningarna och , inte som du har skrivit.
Kolla enhetscirkeln!
hansa skrev:Behöver inte bli så krångligt. Kan vara lättare att skissa cos och sin i ett diagram. Då ser man att i intervallet
har cos bara värdet för argumentet . D v s som ger
...
Nej det resonemanget håller inte. Det är som ska ligga i intervallet, inte .
Samma sak gäller för b-uppgiften.
Jag tycker det underlättar väldigt mycket att veta att orden cosinus och sinus är i alfabetisk ordning, precis som x och y.
okej så mina svar
Antar att det fortfarande handlar om fråga a.Det är inte rätt svar på den fråga som ställts i uppgiften. Man vill bara ha de svar som ligger mellan 0 och inklusive ändpunkterna. Vilka av dina svar ligger i rätt intervall?
okej så det är inte lösningsmängd för uppgift b?
Nej det är inte rätt lösningsmängder.
Ta ett steg i taget och använd enhetscirkeln!
Steg 1: Förenkla ekvationen genom att införa en ny obekant
Steg 2: Använd enhetscirkeln för att hitta ekvationens två lösningar i intervallet .
Steg 3: Använd vetskapen att sinusfunktionen har perioden för att skriva alla lösningar .
Steg 4: Ersätt med och lös ut i de båda lösningsmängderna.
Steg 5: Välj ut det/de värden på konstanten som ger de värden på som ligger i det önskade intervallet.
Det är alltså samma tillvägagångssätt som på a-uppgiften.
Visa alla dina resonemangs- och beräkmingssteg detaljerat.
Jag förstår inte riktigt nu. Om jag löser (sin2x-så får jag
eller är det att jag får
Det blir lite fel när du förlänger med .
Det gäller att .
Sen blandar du ihop vinklar med sinusvärden.
Det gäller inte att .
Däremot gäller att ekvationen har lösningarna
och
Är du med på det?
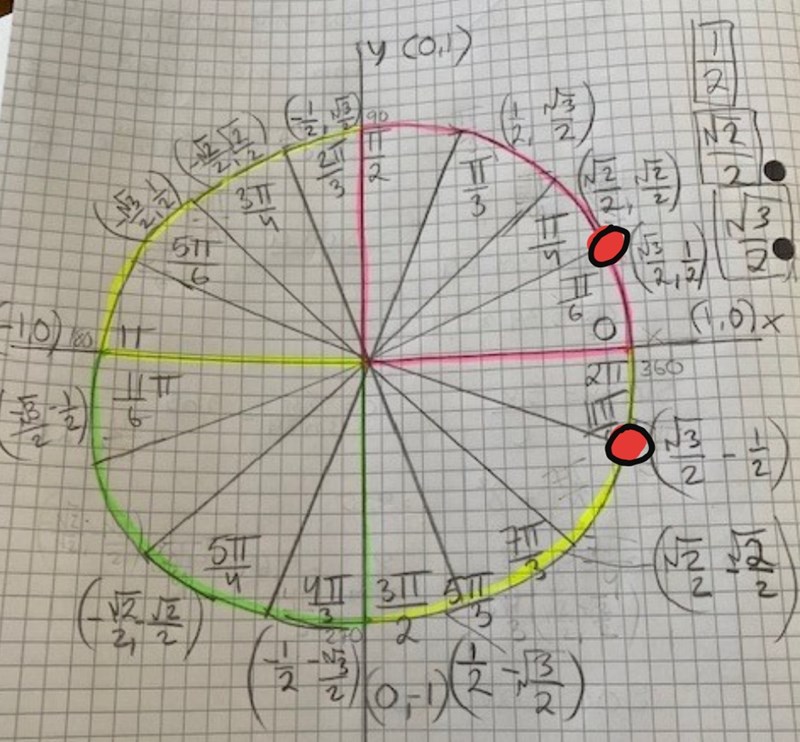
Du kan läsa av detta direkt i enhetscirkeln:
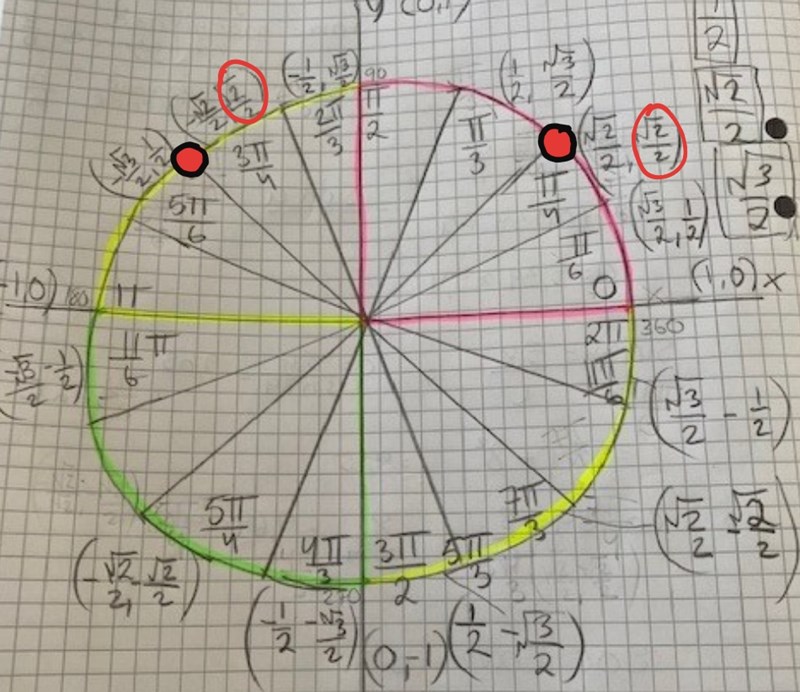
nej känns inte som det.
Ok jag har kompletterat mitt senaste svar med en bild av var lösningarna återfinns i enhetscirkeln. Blir det klarare då eller är det något som du vill fp förtydligat?
hmm okej så lösningsmängden är då:
?
då får jag isf ekvationerna:
Är detta rätt såhär långt?
1) är rätt och uttrycket kan förenklas.
2) är rätt förutom att du har missat att addera termerna och med varandra i högerledet. Sedan kan uttrycket förenklas.
ja skrev fel det ska va x=
förenklat då menar du att det ska se ut såhär:
Ja nästan. Du glömmer att dividera med 2.
ja okej men om jag ska testa detta nu då för vilka x. för ekvation nr 1:
n=-1:
n=1=
n=2
men jag får bara att för n=0 så är det inuti intervallet men inget av dem andra. stämmer det?
Ja det stämmer.
Hittar du någon lösning inom önskat intervall från den andra lösnimgsmängden?
det är bara som ligger i intervallet. Men måste jag inte ha samma nämnare? det var det på den andra uppgiften?
Ja det stämmer.
Nej du måste inte ha samma nämnare på lösningarna.
okej. Tack så jättemycket för all hjälp! :)




