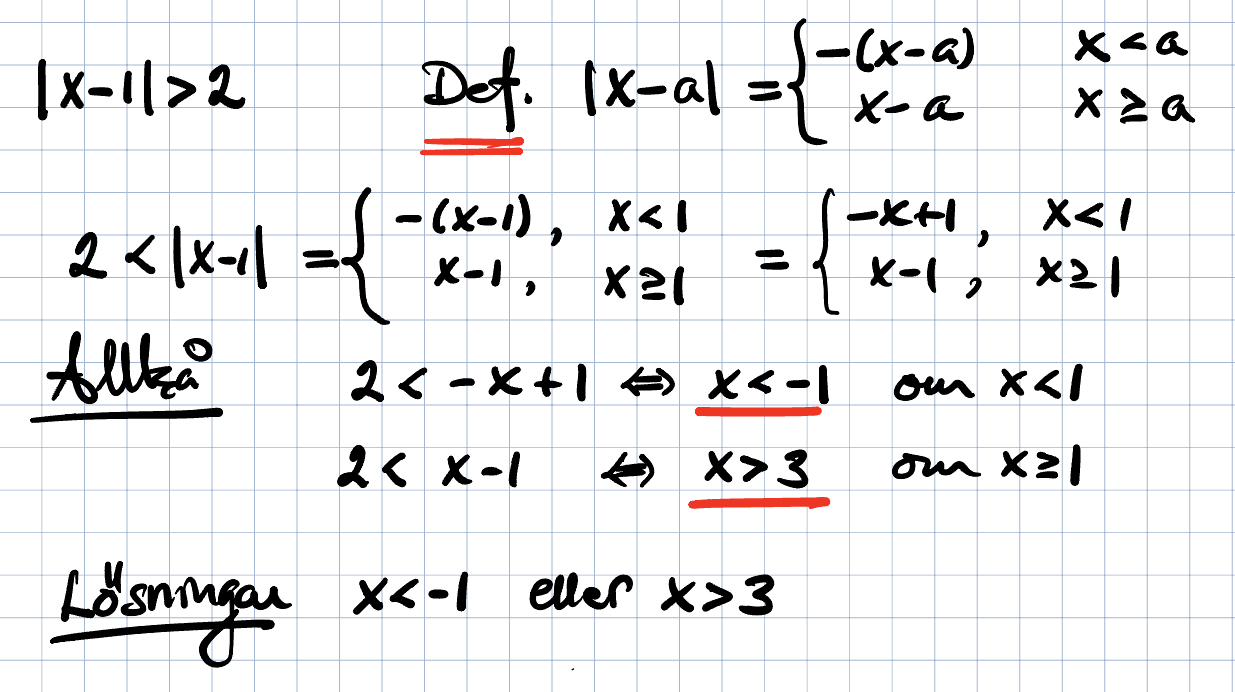"Lös olikheten"
Hej igen.
Hänger inte med på detta. Kan någon förklara?

Mvh
Man delar upp det på två fall.
FAll 1, det innanför beloppstecknet > 0 då har vi helt enkelt
x-1 > 2 att lösa, enkelt x > 3
Fall 2. Det innanför beloppstecknet < 0, dvs x < 1 då har vi ekvationen
1-x > 2 att lösa (vi har tagit bort beloppstecknet men först multiplicerat innehållet med -1 )
1-x > 2 löser vi genom att addera -1 på bägge sidor ger
-x > 1, som sen multipliceras med -1 på bägge sidor, men då måste vi byta riktning på olikhetstecknet, alltså
x < -1
Så vårt svar är
x < -1 och
x > 3
som vi kan verifiera genom att testa i ursprungsuttrycket.
Man kan också lösa uppgiften genom att märka ut +1 på tallinjen och sen gå två steg åt vardera hållet
alltså 1 +2 = 3 och 1 -2 = -1
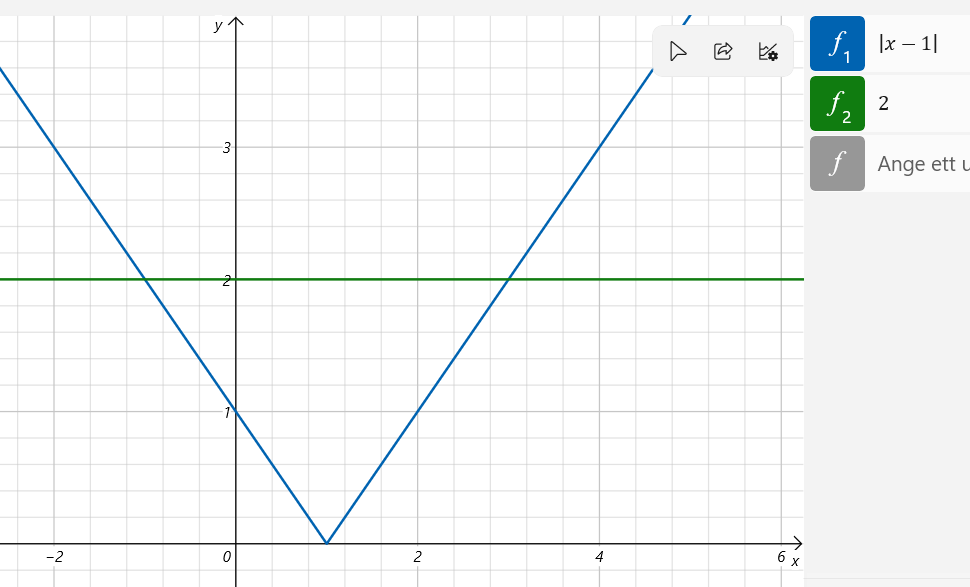
Försök lär dig tolkningen: " |x-a| = R " = "de x som ligger på avstånd R från a"
Då blir denna olikhet lätt.
|x-1|>2 = "De x som ligger längre än 2 steg från 1".
Från 1 på tallinjen ligger alla tal <-1 och alla tal >3 på mer än 2 steg från 1.
Vilken hjärngymnastik.. tog mig en kvart att ta mig till Tures femte rad. Inser att jag lyckats undvika delkapitlet "olikheter". Förstår ju programmeringens <= eller >= eller e g 4 < x <8 och dyl. men av ngn anledning var det här väldigt främmande.
Tack Trinity! Detta hjälpte oerhört. Brukar hjälpa att kunna sätta regeln i ord för mig.. hade en juridisk bakgrund i gymnasiet. :P
Lite som: "f har gränsvärdet *, när x går mot */limes av f(x), när x går mot *, är *"
Behöver förbereda mig inför en god natts sömn vilket nog kan hjälpa. Klurar lite till så att konceptet sätter sig. Brukar ta tid för mig; speciellt under småtimmarna.
Trinity2 skrev:Försök lär dig tolkningen: " |x-a| = R " = "de x som ligger på avstånd R från a"
Då blir denna olikhet lätt.
|x-1|>2 = "De x som ligger längre än 2 steg från 1".
Från 1 på tallinjen ligger alla tal <-1 och alla tal >3 på mer än 2 steg från 1.
PS: Glömde helt bort dig under röstningen i forumet. Du borde givetvis ha delad plats med sictransit och 5p.
Hej igen Ture. Jag har nu "avkrypterat" det och följer logiken. Men kan du förklara eller länka till en resurs som gör att jag förstår det här bättre?
"-x > 1, som sen multipliceras med -1 på bägge sidor, men då måste vi byta riktning på olikhetstecknet, alltså"
Varför byter olikhetstecknet riktning? Tänker på en ekvation hela tiden.
Och varför multiplicerar vi här i "1-x > 2 att lösa (vi har tagit bort beloppstecknet men först multiplicerat innehållet med -1 )"? Förstår ingenting.
maratmatorkin skrev:Hej igen Ture. Jag har nu "avkrypterat" det och följer logiken. Men kan du förklara eller länka till en resurs som gör att jag förstår det här bättre?
"-x > 1, som sen multipliceras med -1 på bägge sidor, men då måste vi byta riktning på olikhetstecknet, alltså"
Varför byter olikhetstecknet riktning? Tänker på en ekvation hela tiden.
Det var inte meningen att förvirra dig med en massa aritmetik, kanske var det meningen att man skulle lösa uppgiften som Trinity visade, vilket ger en bra känsla för hur absolutbelopp fungerar i olikheter.
Nåväl
Den stora fällan när man räknar med olikheter är just det du frågat om. Precis som du antyder, det är nästan som att lösa en ekvation.
Men titta på det här exemplet
2 > 1 vilket uppenbarligen gäller.
Om du nu multiplicerar bägge led med -1, som i en ekvation, får du
-2 > -1 vilket är falskt !
För att det ska bli sant vänder vi på olikhetstecknet !
-2 < -1.
Du kan också titta på det exemplet vi hade,
-x > 1
addera x på bägge sidor ger
0 > 1+x , subtrahera sen 1 i bägge led och du får
-1 > x
Alltså när du multiplicerar en olikhet med ett negativt tal (eller dividerar) ska du alltid vända på olikhetstecknet. Det här måste stå någonstans i din lärobok.
sen din andra fråga
Och varför multiplicerar vi här i "1-x > 2 att lösa (vi har tagit bort beloppstecknet men först multiplicerat innehållet med -1 )"? Förstår ingenting.
När vi räknar med belopp och inte direkt ser lösningen på tallinjen som Trinity visade så delar vi upp det i 2 fall
I vårt exempel har vi beloppet av x-1
om x >= 1 är x-1 alltid positivt och vi kan helt sonika ta bort beloppstecknet.
när x < 1 är innehållet innanför beloppstecknet negativt, för att få det positivt kan man multiplicera med -1 vilket är samma sak som att byta tecken på alla termer som finns innanför beloppstecknet
Ture skrev:
Alltså när du multiplicerar en olikhet med ett negativt tal (eller dividerar) ska du alltid vända på olikhetstecknet. Det här måste stå någonstans i din lärobok.
Bra att veta! Och väldigt bra demonstrerat. Tack! Vet inte hur jag missat detta ända upp till nu men det har dykt upp i ett par uppgifter förr som inte varit så betydande att det lett till någon större konsekvens förrän nu.
Denna video hjälpte också:
Det Trin förklarade https://youtu.be/MoVRVkoamGM?t=337
Och Ture (fast i videon saknade jag det jag undrade tidigare) https://youtu.be/MoVRVkoamGM?t=597
Försöker "internalisera" detta och ger mig på uppgiften en sista gång utan kryckor så stänger jag tråden om jag inte har fler funderingar.
Ture skrev:när x < 1 är innehållet innanför beloppstecknet negativt, för att få det positivt kan man multiplicera med -1 vilket är samma sak som att byta tecken på alla termer som finns innanför beloppstecknet
Jag försökte räkna om uppgiften men vände tecken två gånger och fick samma svar som när inte gjorde något alls med tecknet. Och det är nog det här jag inte förstår. Du sa tidigare (och bevisade) att när vi multiplicerar eller dividerar med -1 så byter vi tecken. Men här multiplicerar du med -1 men byter inte tecken.
Hm, denna gång fick jag till det!
Det verkar som att du har multiplicerat med -1 men sedan med -1 igen i slutet och det leder ju till samma slutsats. Det kanske finns en poäng här jag missar.. väldigt märkligt sätt att uttrycka det.

maratmatorkin skrev:Ture skrev:när x < 1 är innehållet innanför beloppstecknet negativt, för att få det positivt kan man multiplicera med -1 vilket är samma sak som att byta tecken på alla termer som finns innanför beloppstecknet
Jag försökte räkna om uppgiften men vände tecken två gånger och fick samma svar som när inte gjorde något alls med tecknet. Och det är nog det här jag inte förstår. Du sa tidigare (och bevisade) att när vi multiplicerar eller dividerar med -1 så byter vi tecken. Men här multiplicerar du med -1 men byter inte tecken.
Hm, denna gång fick jag till det!
Det verkar som att du har multiplicerat med -1 men sedan med -1 igen i slutet och det leder ju till samma slutsats. Det kanske finns en poäng här jag missar.. väldigt märkligt sätt att uttrycka det.
Räkna så här, utan multiplikation eller division.
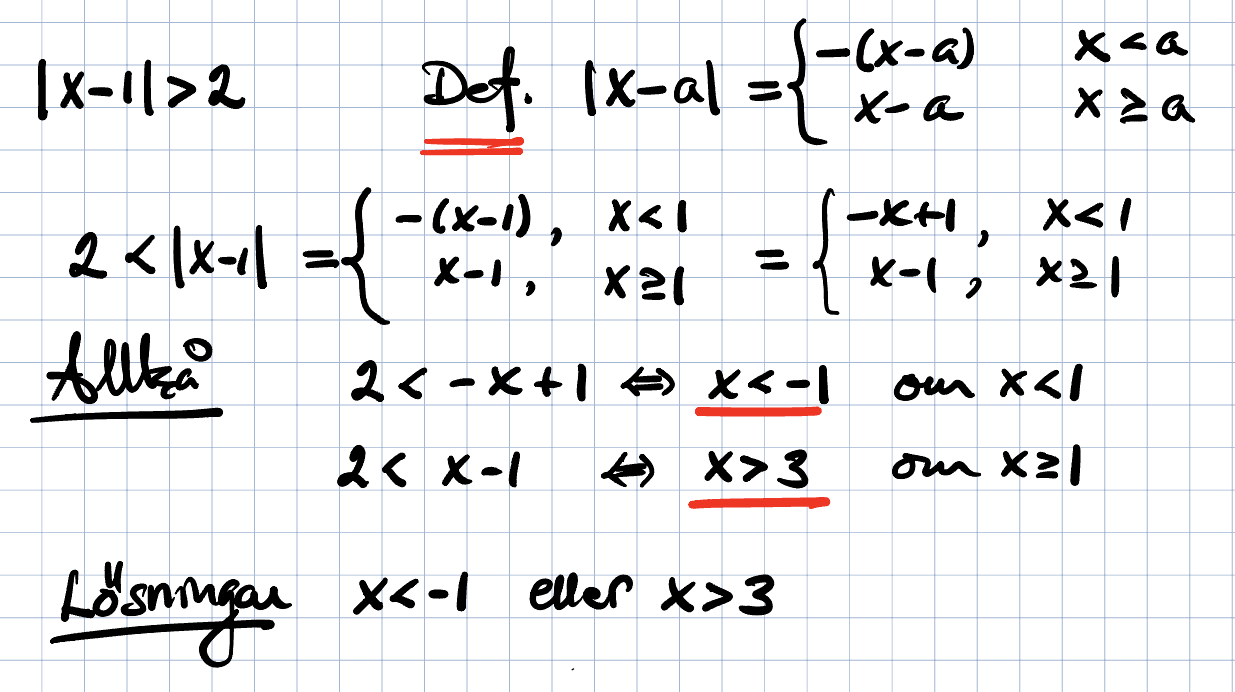
Trinity2 skrev:maratmatorkin skrev:Ture skrev:när x < 1 är innehållet innanför beloppstecknet negativt, för att få det positivt kan man multiplicera med -1 vilket är samma sak som att byta tecken på alla termer som finns innanför beloppstecknet
Jag försökte räkna om uppgiften men vände tecken två gånger och fick samma svar som när inte gjorde något alls med tecknet. Och det är nog det här jag inte förstår. Du sa tidigare (och bevisade) att när vi multiplicerar eller dividerar med -1 så byter vi tecken. Men här multiplicerar du med -1 men byter inte tecken.
Hm, denna gång fick jag till det!
Det verkar som att du har multiplicerat med -1 men sedan med -1 igen i slutet och det leder ju till samma slutsats. Det kanske finns en poäng här jag missar.. väldigt märkligt sätt att uttrycka det.
Räkna så här, utan multiplikation eller division.
Tack så hemskt mycket! Lär mig bäst när det är skrivet som i formelbladet i "allmän/generisk" form rätta mig gärna om det heter annorlunda. Då kan jag applicera det överallt och bara memorera dessa "regler". :-) Sparar detta i urklipp. Och nu förstår jag det fullt ut! :)