Lös olikheten
Fråga: Lös olikheten
|x-1| < |x-2|
Mitt svar: x < ( 1, 3/2 )
är osäker på mitt svar är det någon som kan rätta detta, och ge rätt svar med tips?
Är osäker på vad du menar med ditt svar.
Cemark skrev :Är osäker på vad du menar med ditt svar.
Är då (3/2) större än 1 och 1 större än x, är alltså osäker själv på mitt svar, vet ej om det är rätt eller fel. Det kanske finns ett annat rätt svar.
Hur kom du fram till det?
Cemark skrev :Hur kom du fram till det?
försökte lösa uppgiften genom tips på google, kanske räkande helt fel... om du kan, skulle du kunna lösa eller ge tips på hur jag kommer fram till lösningen, all hjälp uppskattas.
Kan du utläsa vad t ex abs(x-2)<5 betyder?
Just den här typen av olikheter brukar vara enklast att lösa "geometriskt"!
Tänk dig en tallinje:
 Om x betecknar ett godtyckligt tal på tallinjen, så kommer |x-1| vara avståndet mellan x och talet 1, medan |x-2| kommer vara avståndet mellan x och talet 2.
Om x betecknar ett godtyckligt tal på tallinjen, så kommer |x-1| vara avståndet mellan x och talet 1, medan |x-2| kommer vara avståndet mellan x och talet 2.
Att lösa olikheten |x-1|<|x-2| kommer nu motsvara att hitta alla x sådana att avståndet från x till 1 är mindre än avståndet från x till 2.
Du ser kanske direkt att svaret är alla att alla x<1.5 har "närmare till" 1 än de har till 2. Bra i så fall! Om inte, eller om du inte är helt övertygad kan vi börja med att svara på en något enklare fråga:
Vilka x har lika långt till 1 som till 2? Dvs. vilka x uppfyller |x-1|=|x-2|? Det är ju så klart precis det tal som ligger mitt emellan 1 och 2, dvs. medelvärdet: 1,5.
 Kan du nu argumentera för att alla x som ligger till vänster om 1.5 har närmare till 1 än till 2? Dvs. att lösningen till |x-1|<|x-2| är x<1.5:
Kan du nu argumentera för att alla x som ligger till vänster om 1.5 har närmare till 1 än till 2? Dvs. att lösningen till |x-1|<|x-2| är x<1.5:
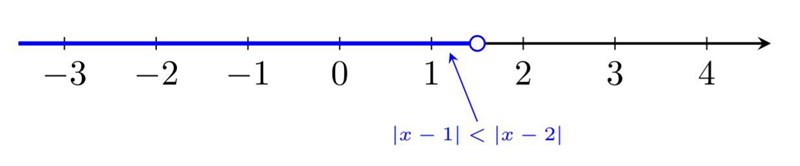
Förslag: Prova att lösa |x-1|<|x-3|, |x-1|>|x-3| och |x+2|<|x+1| [samma sak som |x-(-2)|<|x-(-1)| ] på det här sättet. Du kan kontrollera dina svar med Wolfram Alpha.
Ett annat tips är att lösa uppgiften grafiskt:
Rita graferna till y1=|x-1| och y2=|x-2|.
Lösningsmängden är alla x för vilka y1 ligger under y2.
Välkommen till Pluggakuten!
Du behöver studera tre fall.
Fall 1. Talet x är mindre än talet 1. Då ser olikheten ut såhär:
1-x<2-x
Detta är samma sak som olikheten , som alltid är sann. I detta fall är olikheten sann för alla tal som är mindre än 1.
Fall 2. Talet ligger mellan talen och Då ser olikheten ut såhär:
Detta är samma sak som olikheten I detta fall är den givna olikheten sann för alla tal som ligger mellan och
Fall 3. Talet är större än talet Då ser olikheten ut såhär:
Detta är samma sak som olikheten som är falsk. I detta fall är den givna olikheten inte sann för något tal som är större än talet
Resultat: Olikheten är sann för alla tal som är mindre än
Albiki




