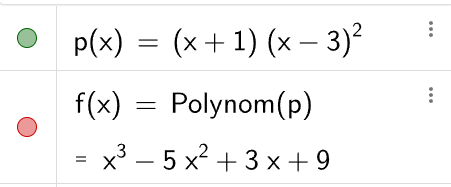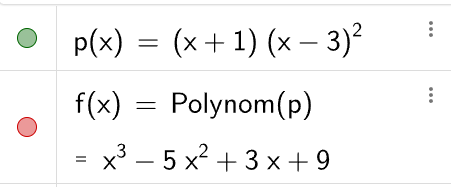Lösa k ur ett polynom i faktorform i GeoGebra CAS?
Hej.
förut var vi inne på hur en förstagradare gick att lösa i GeoGebra men denna metod funkar inte här tyvärr.
 mvh
mvh
Testa att skriva ett multplikationstecken (eller åtminstone ett mellanslag) mellan k och (x+1) i definitionen av p(x).
I din skärmbild verkar GeoGebra tolka uttrycket k(x+1) inte som talet k multiplicerat med (x+1), utan som funktionen k där man satt in (x+1)
Vad LuMa07 sade ...
Här har jag skippat faktorn k eftersom jag bara är intresserad av det moniska polynomet (där koefficienten för x3 är =1).
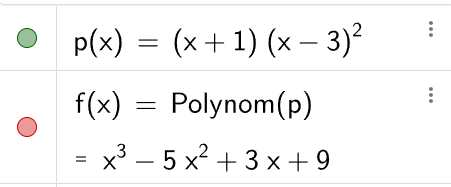
Jag tycker uppgiften är lite märkligt formulerad eftersom man efterfrågar "polynomet". Det går ju att välja ett godtyckligt värde på k och få hur många polynom som helst.
Tillägg: 19 sep 2025 20:09
Som mycket riktigt kommenterats nedan finns det ett villkor till, nämligen (1,16). Slarvigt läst av mig.
sictransit skrev:Vad LuMa07 sade ...
Här har jag skippat faktorn k eftersom jag bara är intresserad av det moniska polynomet (där koefficienten för x3 är =1).
Jag tycker uppgiften är lite märkligt formulerad eftersom man efterfrågar "polynomet". Det går ju att välja ett godtyckligt värde på k och få hur många polynom som helst.
Men p(1)=16 ?
Trinity2 skrev:sictransit skrev:Vad LuMa07 sade ...
Här har jag skippat faktorn k eftersom jag bara är intresserad av det moniska polynomet (där koefficienten för x3 är =1).
Jag tycker uppgiften är lite märkligt formulerad eftersom man efterfrågar "polynomet". Det går ju att välja ett godtyckligt värde på k och få hur många polynom som helst.
Men p(1)=16 ?
My bad! Så går det när man inte läser hela uppgiften.
Jag hittar inget bra sätt att anpassa ett polynom av grad tre till punkter, åtminstone inte med en dubbelrot.
Det gick bra med en "slider" för k och sedan använda funktionen "skärning" för att se när man träffar (1,16). Inte så smidigt jag ville ha det, men åtminstone ett sätt.
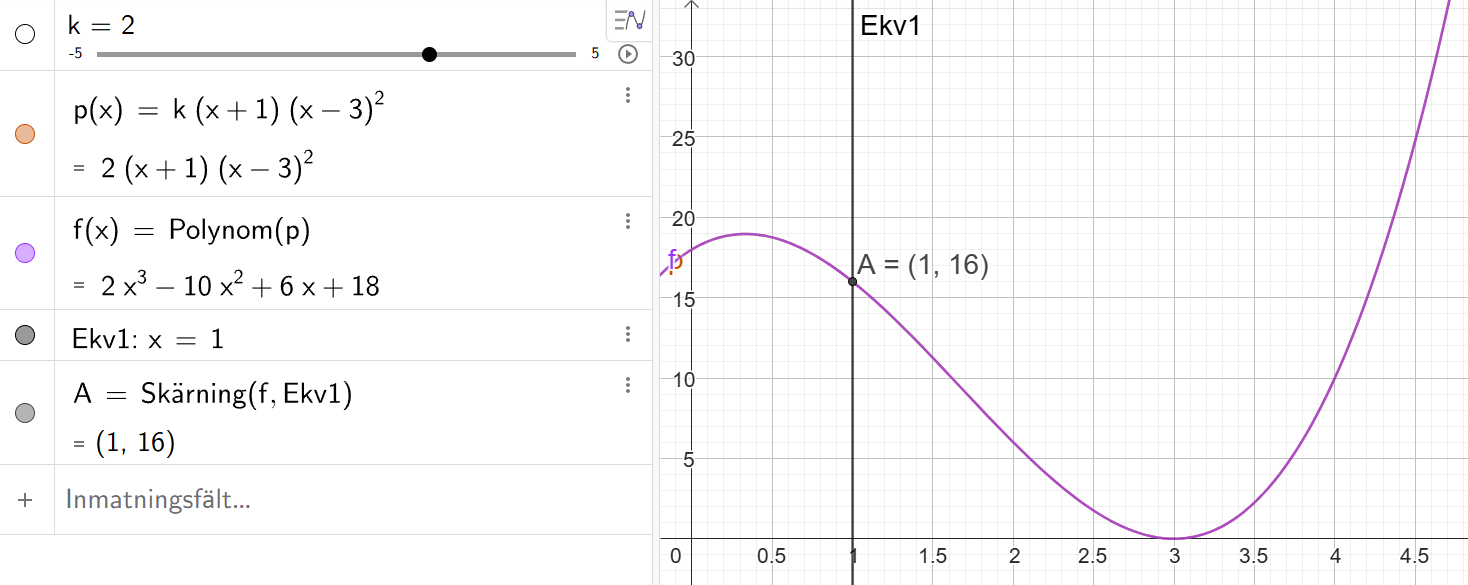
LuMa07 skrev:Testa att skriva ett multplikationstecken (eller åtminstone ett mellanslag) mellan k och (x+1) i definitionen av p(x).
I din skärmbild verkar GeoGebra tolka uttrycket k(x+1) inte som talet k multiplicerat med (x+1), utan som funktionen k där man satt in (x+1)
Japp. Det fungerade!:)