lösa komplex andragradsekvation
Hej!
Jag vill lösa ekvationen .
I min kursbok använder dem sig av kvadratkomplettering som steg 1.
Men då är koefficenten för z ett enklare tal som t.ex .
Jag har försökt lösa min uppgift genom kvadratkomplettering. Och då får jag
Men det blir så komplicerat jag kommer inte vidare, finns det någon som vet en bättre metod för att lösa denna typ av ekvation?
Att lösa andragradsekvationer med komplexa koefficienter är ett större arbete så det går inte att komma undan.
Ditt första steg är bra men det du har landat i är att du nu måste lösa en andragradsekvation på formen
Och var man går härifrån beror på hur man vill uttrycka svaret. Om det räcker att svaret är uttrycket med artimetiska operationer och kvadratrötter så kunde man ju svara
DET ÄR ABSOLUT INGET FEL MED DETTA då det är en sluten formel som kan användas för att beräkna lösningen numeriskt. Men om man verkligen vill ha svaret på kartesisk form så behöver man finna lösningen till
på kartesisk form vilket är en överaskande mödosam uppgift även om det inte är så svårt rent mekaniskt. Rent allmännt så är lösningarna till en ekvation på formen
på formen
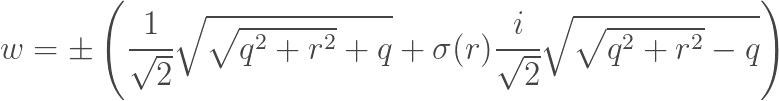
där avser tecknet hos så exempelvis (Reserverar mig för slarvfel) Om övningens mål är att härleda detta så kan vi diskutera det men är inte en uppgift som brukar dyka upp då det inte verkar finnas så stor praktisk nytta i denna formel.
SeriousCephalopod skrev:Att lösa andragradsekvationer med komplexa koefficienter är ett större arbete så det går inte att komma undan.
Ditt första steg är bra men det du har landat i är att du nu måste lösa en andragradsekvation på formen
Och var man går härifrån beror på hur man vill uttrycka svaret. Om det räcker att svaret är uttrycket med artimetiska operationer och kvadratrötter så kunde man ju svara
DET ÄR ABSOLUT INGET FEL MED DETTA då det är en sluten formel som kan användas för att beräkna lösningen numeriskt. Men om man verkligen vill ha svaret på kartesisk form så behöver man finna lösningen till
på kartesisk form vilket är en överaskande mödosam uppgift även om det inte är så svårt rent mekaniskt. Rent allmännt så är lösningarna till en ekvation på formen
på formen
där avser tecknet hos så exempelvis (Reserverar mig för slarvfel) Om övningens mål är att härleda detta så kan vi diskutera det men är inte en uppgift som brukar dyka upp då det inte verkar finnas så stor praktisk nytta i denna formel.
Hm svaret ska vara på rektangulär form: z=-2-3i och z=-1-i
Om du vill vill lösa en ekvation på formen
så rekommenderar jag att du helt enkellt definierar där xx,y är okända och substituerar in det i ekvationen
utvecklar parentesen och försöker lösa ut x och y, förslagsvis genom att sätta uttryckets real och imaginärdelar till 0.
Sidospår:
Nu när det visar sig att rötterna är gaussiska heltal (komplexa tal med heltalsdelar) så kan man härleda rötterna på snabbare vis men det är inte en allmänn metod utan råkar bara fungera
Du vet hur det är med rationella rotsatsen att man kan gissa rationella rötter p/q till ett polynom med heltakoefficienter att och . Beviset för det vilar egentligten inte på att det ska vara just heltal utan endast att man kan primtalsfaktorisera saker så samma princip kan appliceras när man har gaussiska heltal.
och motsvarar här
$$p | -(1 + 5i)$$ och
Då är frågan vilka tal p som "delar" -(1 + 5i). För detta behöver man "primtalsfaktorisera" 1 + 5i vilket visar sig gå att göra till
(http://www.wolframalpha.com/input/?i=1+%2B+5i)
Okej så möjliga p som delar detta tal är
Om man testar de olika så antyder alltså facit att
är de två lösningarna.
Hej Fannywi,
Ekvationen har inte de lösningar facit föreslår.
Däremot har ekvationen de lösningar facit föreslår.
Dessutom ger den ekvationen lite enklare räkningar. Jag föreslår därför att du löser den istället.
Guggle skrev:Hej Fannywi,
Ekvationen har inte de lösningar facit föreslår.
Däremot har ekvationen de lösningar facit föreslår.
Dessutom ger den ekvationen lite enklare räkningar. Jag föreslår därför att du löser den istället.
Ja vad dumt. jag har skrivit ett minustecken fel
Jag precis jag tänkte fråga dig också...
Hej!
Som Guggle skrev:
Ekvation du postade har dessa lösningar:
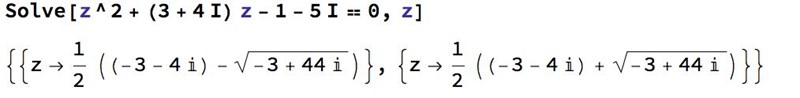
Och det är definitiv inte dessa vi är efter.
Jag hade ingen aning att rationnella sats metod kan användas på komplexa tal, men tillägg till IntelligentSquid metoden, vi brukade använda oss av Snällagemigentillekvation-metoden:
När du kommer till:
(jag kom aldrig där p.g.a nåt irriterande teckenfel, men vi struntar i det...)
Utvekla
Du ser att den reella del är och den imaginära del .
Samtidigt kan du ta absolutbelopp till
Nu kan du skriva en enkel ekvationsystem med:
Nu är det bara att addera, respektive substrahera (1) och (2):
På motsvarande sätt:
Från ekvation (3) ser du att a och b måste ha samma tecken. Antigen är dem båda negativa, eller båda positiva, annars blir inte resultat 1.
Så du har två resultat:
, och .
Ploppar du dom tillbaka i ursprungliga ekvationen:
Edit: definitivt inte lika snyggt som vad IntellectuelOctopus föreslog men snällagemigentillekvation metoden har hjälpt mig mycket.
Edit 2: jag hoppas att det är ingen mer teckenfel från min sida...
dajamanté skrev:Hej!
Som Guggle skrev:
Ekvation du postade har dessa lösningar:
Och det är definitiv inte dessa vi är efter.
Jag hade ingen aning att rationnella sats metod kan användas på komplexa tal, men tillägg till IntelligentSquid metoden, vi brukade använda oss av Snällagemigentillekvation-metoden:
När du kommer till:
(jag kom aldrig där p.g.a nåt irriterande teckenfel, men vi struntar i det...)
Utvekla
Du ser att den reella del är och den imaginära del .
Samtidigt kan du ta absolutbelopp till
Nu kan du skriva en enkel ekvationsystem med:
Nu är det bara att addera, respektive substrahera (1) och (2):
På motsvarande sätt:
Från ekvation (3) ser du att a och b måste ha samma tecken. Antigen är dem båda negativa, eller båda positiva, annars blir inte resultat 1.
Så du har två resultat:
, och .
Ploppar du dom tillbaka i ursprungliga ekvationen:
Edit: definitivt inte lika snyggt som vad IntellectuelOctopus föreslog men snällagemigentillekvation metoden har hjälpt mig mycket.
Edit 2: jag hoppas att det är ingen mer teckenfel från min sida...
Tack detta hjälpte jättemycket.
Jag tror att det är tyvärr en teckenfel, jag försöker undersöka det (har alltid varit skitdåligt med tecken). Men jag lovar att det funkar superbra vanligtvis.
Kanske Guggle eller BrainyBlekfisk hittar vart jag klantrade :(
dajamanté skrev:Jag tror att det är tyvärr en teckenfel, jag försöker undersöka det (har alltid varit skitdåligt med tecken). Men jag lovar att det funkar superbra vanligtvis.
Kanske Guggle eller BrainyBlekfisk hittar vart jag klantrade :(
Ja men jag hittar nog det :)
Det är klart :)! God natt!
dajamanté skrev:Jag tror att det är tyvärr en teckenfel, jag försöker undersöka det (har alltid varit skitdåligt med tecken). Men jag lovar att det funkar superbra vanligtvis.
Kanske Guggle eller BrainyBlekfisk hittar vart jag klantrade :(
 Blekfisk: (egentligen blek fisk)
Blekfisk: (egentligen blek fisk)
Bläckfisk:


dajamanté skrev:
haha jag hittar faktiskt inga , edit jag är slarvig får göra om. ser ju nu att dem svaren inte stämmer med facit
dajamanté skrev:
Jo nu fick jag rätt. Såhär:
Först kvadratkomplettering :
Första steget i uträkningarna efter kvadratkomplettering är göra variabelbytet . (1)
Då får vi ekvationen till . (2)
Om vi sedan sätter i ekvation (2) får vi som du skrev och det ekvationssystemet med ekvationen med absolutbelopp har ju lösningarna och .
Detta är alltså lösningar till ekvation (2).
För att lösa (orginal) ekvationen (1) så vill vi lösa för z och vi har 2 lösningar för w.
Alltså
Så då får vi lösningarna:
och
.
(om jag ordentligt följde ett liknande exempel i min kursbok)
Grymt! Och nu förstod jag äntligen metoden på riktigt!!
dajamanté skrev:Grymt! Och nu förstod jag äntligen metoden på riktigt!!
vad bra :D






