Lösa underligt ekvationssystem
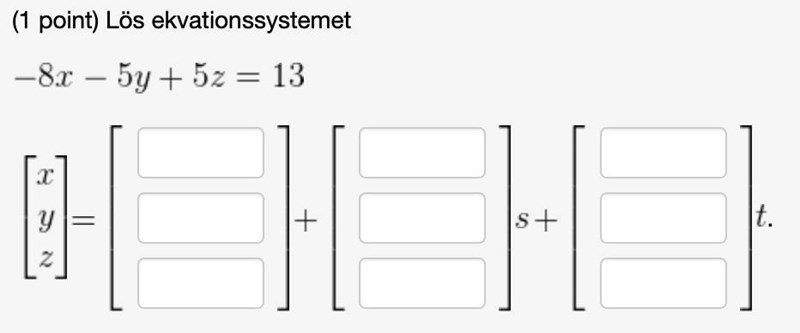
Hur löser man en sådan här lustigkurre? Förstår inte hur man ska lösa ett ekvationssystem med en ekvation och tre variabler.
Din ekvation beskriver ett plan. Det kan också beskrivas med en punkt och två vektorer. Finns flera olika att välja på, försök tex att hitta tre punkter i planet att minusa fram vektorer mellan.
Micimacko skrev:Din ekvation beskriver ett plan. Det kan också beskrivas med en punkt och två vektorer. Finns flera olika att välja på, försök tex att hitta tre punkter i planet att minusa fram vektorer mellan.
Förstår inte vad du menar med en punkt och två vektorer. Du menar väl en punkt och 3 vektorer, där x, y och z är varsin vektor och 13 är punkten. Sedan skriver du jag ska hitta tre punkter i planet att minusa fram vektorer mellan. Vad menar du?
Man kan ignorera den geometriska tolkningen också, och bara lösa på som vanligt tills det tar stopp. Det tar stopp ganska snabbt här, och då kan man använda de variabler som är kvar som parametrar (dvs. döpa om dem till s och t som parametrarna kallas här).
Ett plan har 2 dimensioner. Man börjar någonstans och kan gå åt 2 olika håll, som vi kan kalla framåt och åt sidan. Själva gåendet hör ihop med parametrarna s och t framför vektorerna, som man kan öka och minska för att röra sig.
Om du har 2 punkter i ett plan och minusar dem får du en vektor mellan dem, som också ligger i planet.
För att hitta de 3 punkterna är det bara gissa på x, y, z så att ekvationen för planet är sann.



