Lösningsförslag till u×(nabla×u)
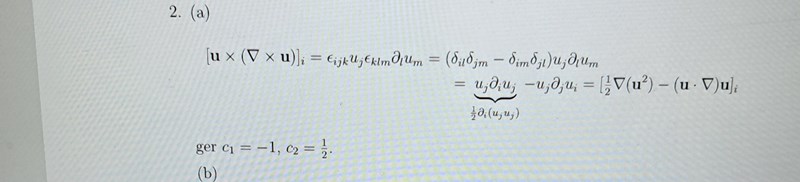
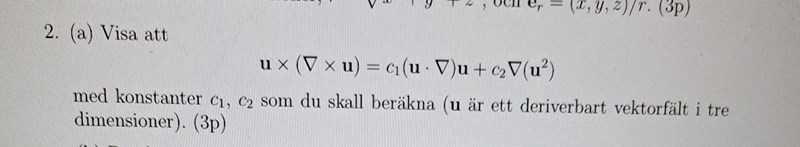
1.Varför kan man inte använda produktregeln på andra termen ujdjui för att få samma som första termen?
2. I lösningen får vi samma uttryck fast c1(u*nabla)u är positivt medan det är negativt i lösningen. Har de kanske glömt att sätta minus framför termen med c1?
1. Du kan använda produktregeln på andra termen, men du får inte samma. Och dessutom leder det dig iväg från det önskade svaret.
2. Nja, läs svaret igen; c1 = -1, c2 = 1/2. Så inget teckenfel, vad jag kan se.
Tillägg: 21 okt 2025 22:16
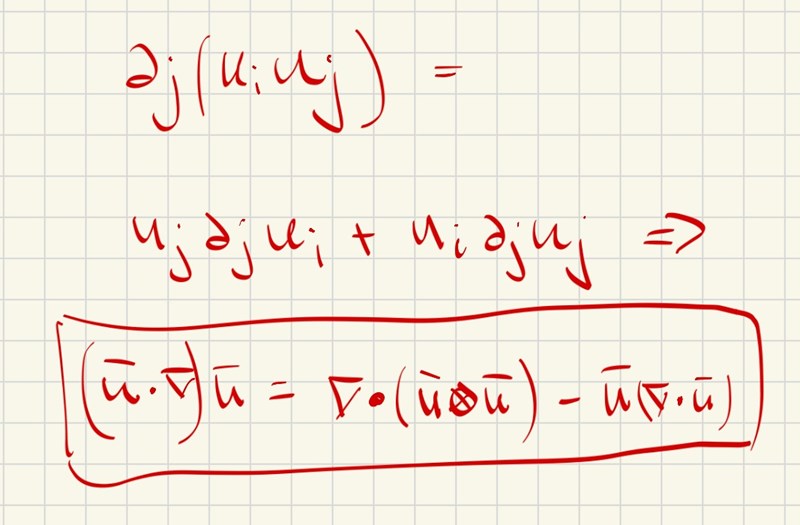
PATENTERAMERA skrev:1. Du kan använda produktregeln på andra termen, men du får inte samma. Och dessutom leder det dig iväg från det önskade svaret.
2. Nja, läs svaret igen; c1 = -1, c2 = 1/2. Så inget teckenfel, vad jag kan se.
Tillägg: 21 okt 2025 22:16
Hur vet man att man inte får samma ? Jo jag ser vad facit fick för värden på c1 och c2. Men i lydelsen ser det ut som att c1 är positivt trots att facit anger ett negativt värde på c1.
Är du med på att ?
Och visst har du ett minustecken framför den termen?
D4NIEL skrev:Är du med på att ?
Och visst har du ett minustecken framför den termen?
Ja jag är med på det. Ja det är minustecken framför den.
Och då blir alltså , om du jämför med problemformuleringen.
Om du har problem med de praktiska räkningarna får du gärna visa hur lång du kommit så kan vi hitta eventuella slarvfel.
destiny99 skrev:PATENTERAMERA skrev:1. Du kan använda produktregeln på andra termen, men du får inte samma. Och dessutom leder det dig iväg från det önskade svaret.
2. Nja, läs svaret igen; c1 = -1, c2 = 1/2. Så inget teckenfel, vad jag kan se.
Tillägg: 21 okt 2025 22:16
Hur vet man att man inte får samma ? Jo jag ser vad facit fick för värden på c1 och c2. Men i lydelsen ser det ut som att c1 är positivt trots att facit anger ett negativt värde på c1.
Var står det att c1 måste vara positivt? Det är något som du läser in utan att det finns något stöd för detta antagande i problemtexten.
Man har ju fått fram en term som innehåller ujdjui = [(u•)u]i. Detta är således redan på en form som vi är ute efter. Jag visade hur man kunde skriva om detta uttryck med liknande teknik (produktregel) som facit använder på den första termen. Men det ger inget av nytta för detta problem.
PATENTERAMERA skrev:destiny99 skrev:PATENTERAMERA skrev:1. Du kan använda produktregeln på andra termen, men du får inte samma. Och dessutom leder det dig iväg från det önskade svaret.
2. Nja, läs svaret igen; c1 = -1, c2 = 1/2. Så inget teckenfel, vad jag kan se.
Tillägg: 21 okt 2025 22:16
Hur vet man att man inte får samma ? Jo jag ser vad facit fick för värden på c1 och c2. Men i lydelsen ser det ut som att c1 är positivt trots att facit anger ett negativt värde på c1.
Var står det att c1 måste vara positivt? Det är något som du läser in utan att det finns något stöd för detta antagande i problemtexten.
Man har ju fått fram en term som innehåller ujdjui = [(u•)u]i. Detta är således redan på en form som vi är ute efter. Jag visade hur man kunde skriva om detta uttryck med liknande teknik (produktregel) som facit använder på den första termen. Men det ger inget av nytta för detta problem.
Ja asså jag antog bara att de menade att c1 var positivt i problemformuleringen, men det facit fick fram var ett negativt värde på c1 så degt är fel antagande av mig att c1 är positivt från början.
När det gäller att skriva om andra uttrycket mha produktregeln så kanske det är onödigt med tanke på att det leder oss bort svaret.


