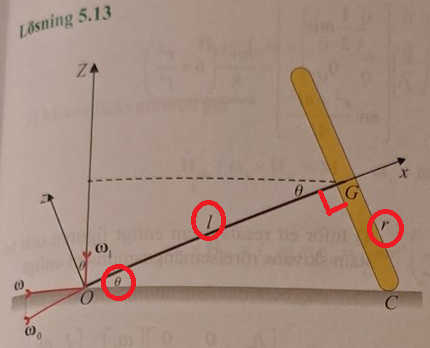
Lösningsförslag till uppgift 5.13


Jag har några frågor gällande lösningen till uppgiften nedan.
1) jag förstår inte varför vg=w1lcostheta samt hur svaret blir till slut lika med v/lez+v/ltanthetaex.
2) de skriver upp och räknar ut wx som jag inte heller är med på varför svaret blir som det blir.
3) i steget där man ska räkna ut vG förstår jag inte var vey kommer ifrån.
4) jag förstår inte steget när de kommer fram vad w0 blir hela vägen till slututtrycket w1/w0

1. G rör sig på en cirkel med radie R = lcos(theta). Vinkelhastigheten är w1. vG = Rw1. De uttrycker eZ i termer av ez och ex.
2. De lägger bara ihop x-komponenterna av w0 och w1.
3. Det står i problemtexten att farten hos G är v. Riktningen är in i pappret, dvs i y-riktningen. Så vG = vey.
4. De utnyttjar att tan(theta) = r/l - figur. Resten är algebra.

PATENTERAMERA skrev:1. G rör sig på en cirkel med radie R = lcos(theta). Vinkelhastigheten är w1. vG = Rw1. De uttrycker eZ i termer av ez och ex.
2. De lägger bara ihop x-komponenterna av w0 och w1.
3. Det står i problemtexten att farten hos G är v. Riktningen är in i pappret, dvs i y-riktningen. Så vG = vey.
4. De utnyttjar att tan(theta) = r/l - figur. Resten är algebra.
Så om jag förstår detta rätt så har cirkeln en rörelse i förhållande till rotationsaxel från G med w1 och sen roterar den även med en hastighet vey som är lika med v_g?
Men hur är tan(thetha)=r/l? Det kan jag inte se i figuren.
tan är motstående/närliggande katet, alltså sin/cos.
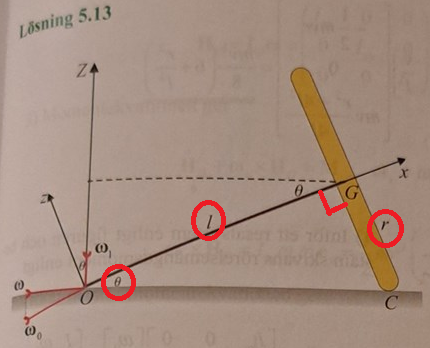
sictransit skrev:tan är motstående/närliggande katet, alltså sin/cos.
Ah ok. Jag såg inte det var rät vinkel vid G.
Hm jag förstår inte riktigt hur vgär lika med vey? jag är med på att de säger att v_g har en konstant fart v men kan ej se hur man avgör riktningen dvs in i pappret (ey) i detta fall. Jag kan liksom tänka mig om vi använder hastighetsamband för att hitta denna konstanta fart som : vg=vc-w0ex×rez=0+w0rey=vey. En annan sak jag också undrar är var v i täljaren kommer ifrån när de löser ut w1 i första steget av lösningen?

Det blir fel eftersom du använder w0 istället för w.
Lättare är att utnyttja
vG = vO + (w1eZ - w0ex) x lex.
Man visar att w1 = v/(lcos(theta)), då blir w1 = veZ/(lcos(theta)).
PATENTERAMERA skrev:Det blir fel eftersom du använder w0 istället för w.
Lättare är att utnyttja
vG = vO + (w1eZ - w0ex) x lex.
Man visar att w1 = v/(lcos(theta)), då blir w1 = veZ/(lcos(theta)).
Hm ok. Vad är skillnaden om vi utnyttjar v_c eller v_o? Jag tänker om vi utnyttjar v_c med kroppens w som då är w1+w0 så blir det ju lika med vey eller? Såhär typ vg=vc+(w1eZ-w0ex)×rez
Jag förstår inte var veZ kommer ifrån? I början hade vi vG=lcosthetaw1. Tänker de att i Z-axeln där w1 roterar så har vi w1=veZ?
Du använder bara -w0ex. Du måste ta med w1 också. Testa båda sätten. Alla vägar bär till Rom.
PATENTERAMERA skrev:Du använder bara -w0ex. Du måste ta med w1 också. Testa båda sätten. Alla vägar bär till Rom.
Se min ändrade inlägg i #8. Ja båda funkar!
På mitt sätt får vi
vG = 0 + w1eZ x lex = lw1eZ x ex = lw1sin(pi/2 + theta)ey = lw1cos(theta)ey. Vilket ger att v = lw1cos(theta).
PATENTERAMERA skrev:På mitt sätt får vi
vG = 0 + w1eZ x lex = lw1eZ x ex = lw1sin(pi/2 + theta)ey = lw1cos(theta)ey. Vilket ger att v = lw1cos(theta).
Jag hänger inte med tyvärr. Menar du hur de får v/lcostheta=w1? Jag förstår fortfarande inte var den där v kommer ifrån. I #8 funkade båda sätt som leder till att vG=vey.
Det står i texten att |vG| = v. Vi har visat att vG = lw1cos(theta)ey. Alltså…
PATENTERAMERA skrev:Det står i texten att |vG| = v. Vi har visat att vG = lw1cos(theta)ey. Alltså…
Ja asså v=lw1costheta=> v/lcostheta=w1. Men här har vi ingen riktning om vi uttrycker w1. Facit använder enhetsvektorer. Jag vet inte om man kan skriva som w1 som w1eZ=v/lcostheta
Nja, w1 = w1eZ. Se figuren.
PATENTERAMERA skrev:Nja, w1 = w1eZ. Se figuren.
Ja precis och w1=(v/lcostheta )*eZ
Du måste skilja mellan skalärer och vektorer.
Så är det något som är oklart?
PATENTERAMERA skrev:Du måste skilja mellan skalärer och vektorer.
Är det inte vad de menar där? beloppet är w1=v/lcostheta, men eftersom vi vill ha vektorn w1 =w1eZ
Dvs använd tex fetstil för vektorer för att skilja från skalärer.
PATENTERAMERA skrev:Dvs använd tex fetstil för vektorer för att skilja från skalärer.
Ok.
PATENTERAMERA skrev:På mitt sätt får vi
vG = 0 + w1eZ x lex = lw1eZ x ex = lw1sin(pi/2 + theta)ey = lw1cos(theta)ey. Vilket ger att v = lw1cos(theta).
Hur fick du pi/2+theta ? Jag får mha högerhandsregeln sin(90-thetha)ey?
Ja, sin(90 - theta) skall det vara, som är lika med cos(theta).
PATENTERAMERA skrev:Ja, sin(90 - theta) skall det vara, som är lika med cos(theta).
Ja precis. Jag tänker i det här steget har de typ glömt att skriva lika med vcosthetaey eller så har de bara hoppat över en del steg för att konstatera att vG=vey

Notera att här utgår man från att man redan vet att vG = vey och vad man är ute efter är att beräkna ett värde på w0.
PATENTERAMERA skrev:Notera att här utgår man från att man redan vet att vG = vey och vad man är ute efter är att beräkna ett värde på w0.
Ja asså beloppet är vg=v men om man ska ha riktningen , borde det inte vara vG=vcosalfaey enligt #23?
Nja, vG = lw1cos(theta)ey, vilket implicerar att v = lw1cos(theta).
PATENTERAMERA skrev:Nja, vG = lw1cos(theta)ey, vilket implicerar att v = lw1cos(theta).
Ja ok. Men varför antar de att det är lika med vey? Tänker de att vey =lw1costhetaey?
De antar ingenting. Du får ju givet i problemet att farten hos G är v. Sedan beräknar vi att vG = lw1cos(theta)ey. Således måste vi ha att v = lw1cos(theta). Vilket ger ett samband mellan v och w1.
PATENTERAMERA skrev:De antar ingenting. Du får ju givet i problemet att farten hos G är v. Sedan beräknar vi att vG = lw1cos(theta)ey. Således måste vi ha att v = lw1cos(theta). Vilket ger ett samband mellan v och w1.
Jo men det är jag med på. Jag bara stör mig på att det står lika med vey. Det står inte direkt givet i informationen att det är i den riktningen så jag vet tyvärr inte var de får det ifrån. Jag hade nog bara skrivit att det är lika med v för att jobba vidare med w0 i det där steget.
Eftersom vi räknat fram att vG är riktad i y-riktningen måste det bli att vG = vey. Vad annars?
PATENTERAMERA skrev:Eftersom vi räknat fram att vG är riktad i y-riktningen måste det bli att vG = vey. Vad annars?
Ja okej jag trodde inte det var så man tänkte eller så de menade i lösningen. Innan var det alltså inte rätt när jag trodde lw1=v så man kunde bara komma fram till att vG= vcosthetaey.
Nej, det är inte rätt att lw1 = v.
PATENTERAMERA skrev:Nej, det är inte rätt att lw1 = v.
Ja precis. Det är alltså en annann hastighet nämligen v1 kanske, men längd gånger vinkelhastighet ska väl ge en hastighet ?
Ja längden är lcos(theta), då blir det rätt.