Lutande plan, lutningsvinkel
En låda står på ett lutande plan. Friktiontalet mellan lådan och planet är 0.45. Hur stor måste lutningvinkeln minst vara för att lådan ska börja glida?
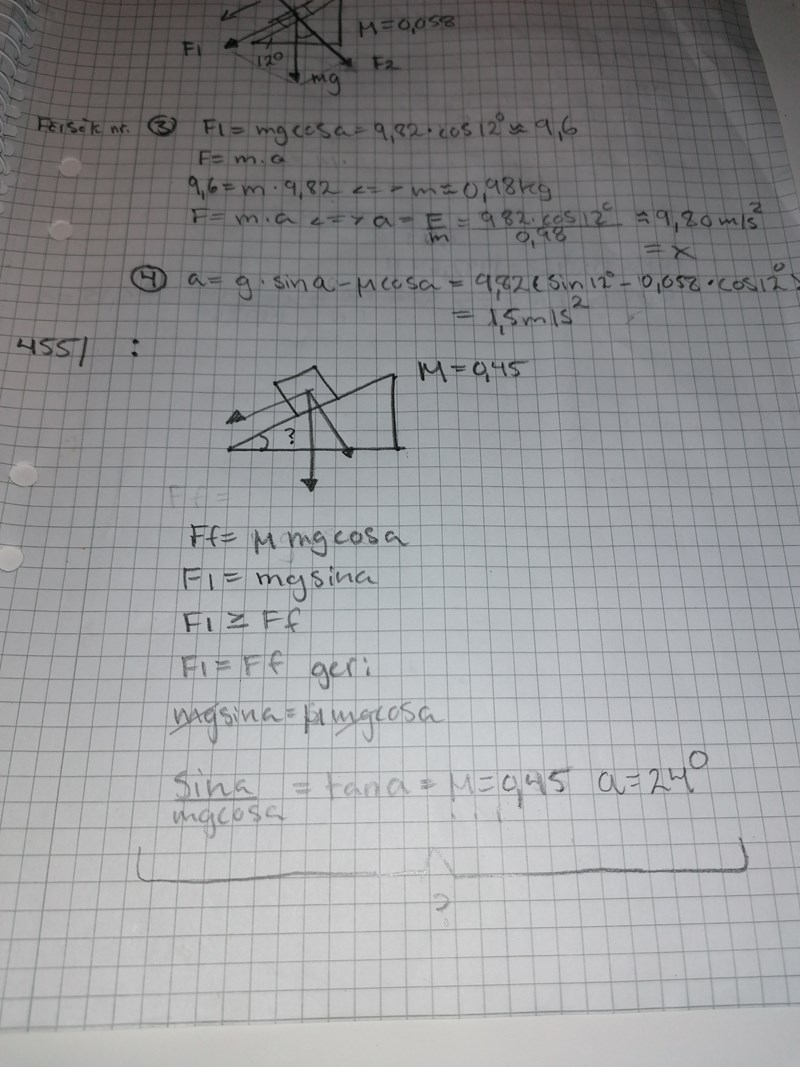
Jag skrev av den sista från lösningsförslaget. Kan någon snälla förklara?
Om lådan glider måste tyngdkraftens komponent längs med planet vara större än eller lika med friktionskraften. Tyngdkraftens komponent längs med planet är:
Friktionskraften är normalkraften gånger friktionstalet. Normalkraften är lika stor som tyngdkraftens komponent normal till planet vilken är:
Vi får friktionskraften som:
Villkoret för glidning blir då:
Vi stryker mg på båda sidor och dividerar med vilket ger:
Vi får slutligen att:
Tack för hjälpen hör du! Varför blir tan^-1 *My?
Ebola skrev:Om lådan glider måste tyngdkraftens komponent längs med planet vara större än eller lika med friktionskraften. Tyngdkraftens komponent längs med planet är:
Friktionskraften är normalkraften gånger friktionstalet. Normalkraften är lika stor som tyngdkraftens komponent normal till planet vilken är:
Vi får friktionskraften som:
Villkoret för glidning blir då:
Vi stryker mg på båda sidor och dividerar med vilket ger:
Vi får slutligen att:
Du har ju som Ebola skrev: .
Lös ut
Alexanderyin03 skrev:Tack för hjälpen hör du! Varför blir tan^-1*My?
Känner du till att ?
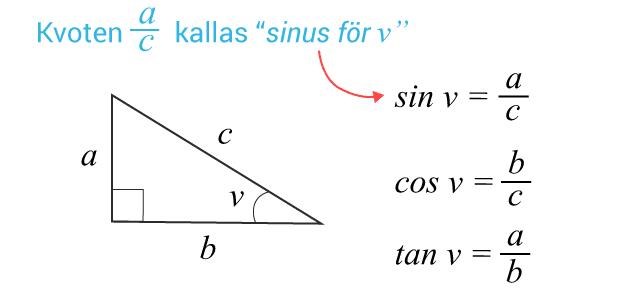
Om du sedan har får du:
Detta är arctangens-funktionen och den har du på din miniräknare:

Ebola skrev:Alexanderyin03 skrev:Tack för hjälpen hör du! Varför blir tan^-1*My?
Känner du till att ?
Om du sedan har får du:
Detta är arctangens-funktionen och den har du på din miniräknare:
Tack för hjälpen!!!



