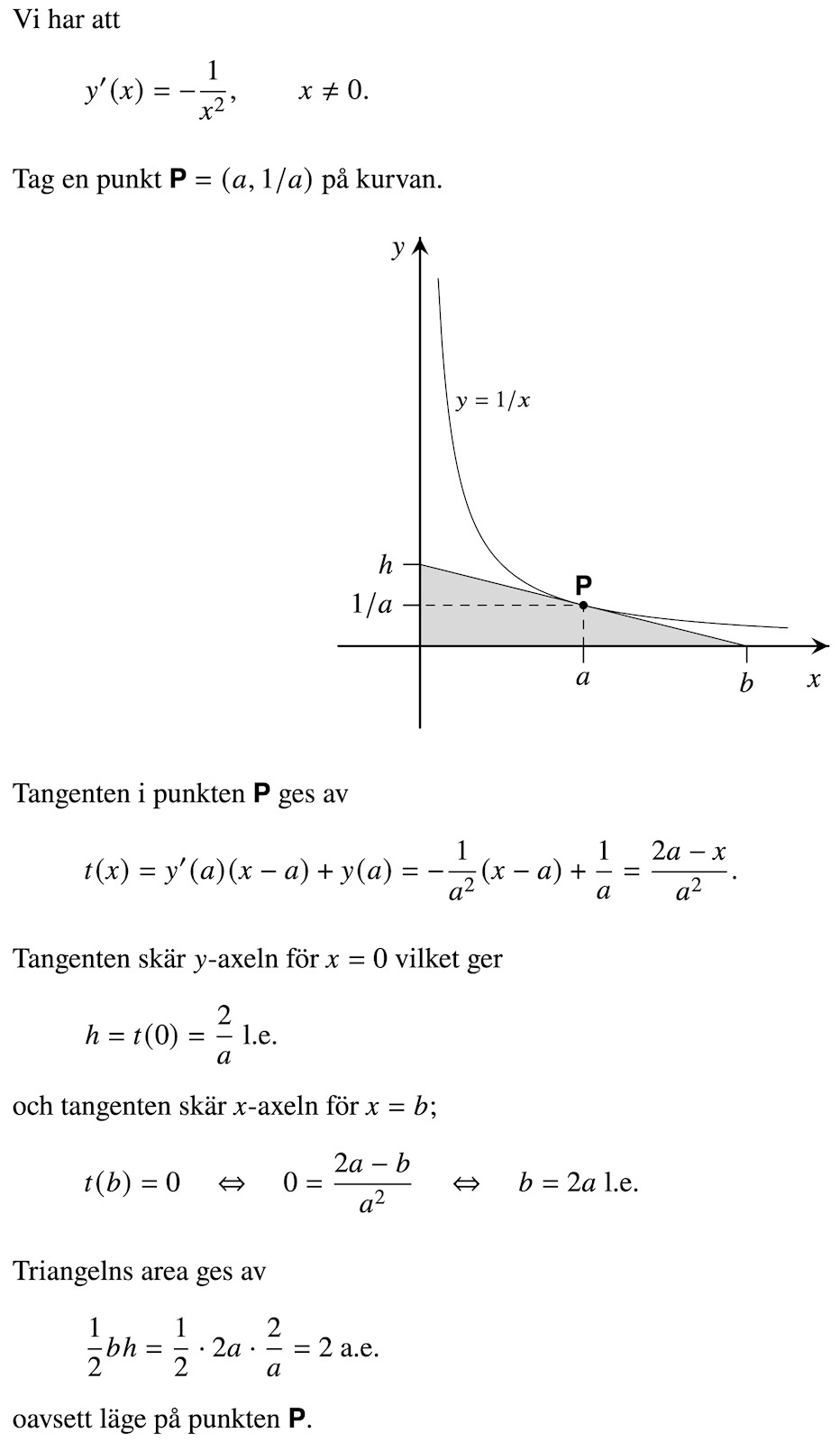
Lutning och area av punkter
Hej,
Denna blev mörk,men man ser ändå vad som står mestadels
Lite klurig, om man inte e van vid den. Man ska derivera kurvan och så har man den rätal linjen y=kx+m där man ska få ut k vilket (väl är?) y2-y1/x2-x1?
Men här har man väl bara ett y respektive ett x-värde?
Hur går stegen till här?
Mvh/H
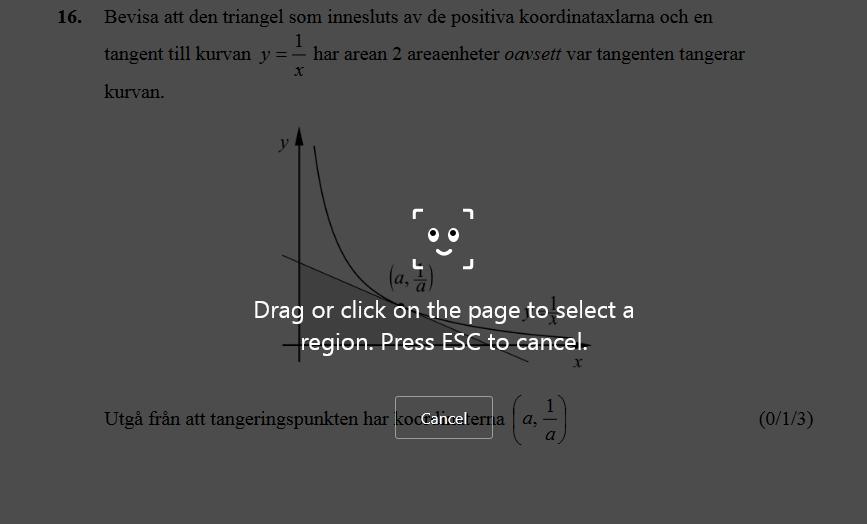
Tangentens lutning (k-värde) är derivatan i punkten (a, 1/a).
Vilket värde har derivatan i punkten?
Ska man förstå derivera och sedan sätta in a?
y=1/x =x upphöjt till minus 1 då man flyttat upp x:et som man gör vid derivering?
y prim= x upphöjt till minus 2?
y prim( a)= a upphöjt till minus 2?
Nej, vet inte vad jag håller på med....ska man derivera funktionen eller punkten a,1/a)
Mvh/H
först
Du har fått tipset förut, så använd det gärna: om du vill rätta någonting i ett inlägg inom en timme så kan du använda Redigera-länken, nere till höger.
Henrik 2 skrev:Ska man förstå derivera och sedan sätta in a?
y=1/x =x upphöjt till minus 1 då man flyttat upp x:et som man gör vid derivering?
y prim= x upphöjt till minus 2?
y prim( a)= a upphöjt till minus 2?
Nej, vet inte vad jag håller på med....ska man derivera funktionen eller punkten a,1/a)
Mvh/H
Hej.
Först lite fler tips på hur du kan skriva så att det blir lättare för oss att förstå vad du menar:
- Använd tecknet ^ för att indikera "upphöjt till". Exempel x2 kan skrivas x^2.
- Använd parenteser för att hålla ihop delar som hör ihop. Exempel: Skriv a^(-2) när du menar a-2.
===========
Nu till själva uppgiften:
Om y = 1/x, dvs y = x^(-1), så är derivatan y' = -1/x2, dvs (-1)*x^(-2)
Det betyder att den tangent som tangerar grafen i punkten (a, 1/a) har lutningen k = -1/a2 (dvs (-1)*a^(-2)).
Med hjälp av denna lutning kan du nu ta fram en ekvation på formen y = kx+m för tangenten.
Nästa steg är att ra reda på vid vilken y-koordinat tangenten skär y-axeln och vid vilken x-koordinat tangenten skär x-axeln.
Då har du allt du behöver för att ta fram ett uttryck för triangelns area.
Hej L,
Förstår inte vad jag ska rätta, redigera i ett inlägg, kan du förklara, exempel på det jag gör/skriver som jag ska göra ett nytt inlägg till så jag förstår?
Mvh/H
Hej Y,
Ok, ska försöka använda mig av symbolerna, men hittar dem inte ibland så skriver i bokstäver,har det så stor betydelse när man ser vad jag skriver i bokstäver, dock så förstår jag att det e bra om jag använder mig av parenteser ibland?
Mvh/H
P.s ska kika din förklaring..
Men varför e det behövligt att skriva med parentes när man tar upphöjt?
Mvh/H
Henrik 2 skrev:Men varför e det behövligt att skriva med parentes när man tar upphöjt?
Mvh/H
Om du skriver 2^2*3 så betyder det (2^2)*3, vilket ör lika med 4^3.
Men om du egentligen menar 2^6 så måste du skriva 2^(2*3)
Henrik 2 skrev:Ok, ska försöka använda mig av symbolerna, men hittar dem inte ibland
Vilken sorts enhet använder du?
Dator? I så fall: Widows, Mac eller Chromebook?
Telefon? I så fall: iPhone eller Android?
Ok, 1:an e kvar.
Så då har man lutningen i punkten vilket blir k=-1/a2
Man sätter in a istället för x. Och nu ska man ta fram ekvationen för tangenten med y=kx+m. Då ska man få ut y och x...o ser var den skär y och x-axeln.
x -1 = -1/a2 +m är det korrekt?
Jo, jag e med på vad du menar med parenteserna i dessa fall, så man kan förstå vad man ska räkna på.
Windows e det väl, så dålig med/på operativsytem.
Henrik 2 skrev:Förstår inte vad jag ska rätta, redigera i ett inlägg, kan du förklara, exempel på det jag gör/skriver som jag ska göra ett nytt inlägg till så jag förstår?
Det hör (se bild nedan):
Du skrev ett inlägg kl 22:35.
Durekt efter det så skrevbdu ett till inlägg enbart med ordet "först".
Jag antar att det var avsett att förtydliga att du menar "först" istället för "förstå" i det ursprungliga inlägget.
Då hade det varit bättre om du hade redigerat det ursprungliga inlägget och korrigerat det.
Aha, precis, så istället för nytt inlägg,redigera det gamla, e med på det.
Henrik 2 skrev:Aha, precis, så istället för nytt inlägg,redigera det gamla, e med på det.
Just så.
Vart redigerar man ett inlägg, vet inte om jag ser det?
Mvh/H
Henrik 2 skrev:Hej L,
Förstår inte vad jag ska rätta, redigera i ett inlägg, kan du förklara, exempel på det jag gör/skriver som jag ska göra ett nytt inlägg till så jag förstår?
Mvh/H
Laguna menar att du borde ha redigerat ditt inlägg #3 istället för att göra ett nytt inlägg med bara ett enda ord i.
EDIT: Jag skrev detta innan jag läst igenom hela tråden och sett att andra redan har påpekat detta. Nu redigerar jag detta inlägg (jag tryckte på "redigera" längst ner i inlägget). Om jag hade vänta för länge, så att redigeringsmöjligheten hade försvunnit, hade jag kunnat "kommentera" mitt inlägg istället.
Yes, förstår.
Henrik 2 skrev:Ok, 1:an e kvar.
Så då har man lutningen i punkten vilket blir k=-1/a2
Man sätter in a istället för x. Och nu ska man ta fram ekvationen för tangenten med y=kx+m. Då ska man få ut y och x...o ser var den skär y och x-axeln.
x -1 = -1/a2 +m är det korrekt?
Nej, det stämmer inte.
Tangentens ekvation är y = -(1/a^2)x+m.
Du behöver nu bestämma värdet på m.
Det kan du göra genom att du känner till koordinaterna för en punkt på linjen, nämligen tangeringspunkten (a, 1/a).
Hej Henrik,
Jag är imponerad av ditt driv att ställa många frågor och jobba igenom dessa, men jag tror att många drar sig ifrån att hjälpa dig på grund av att dina inlägg och trådar blir så stökiga av flera orsaker:
- Du använder inte korrekt matematisk notation. Det blir svårt att gissa till vad du menar.
- Du korrigerar stavfel genom att posta enskilda ord eller kommentarer som stökar upp tråden ännu mer.
- Du visar sällan på ett tydligt sätt hur du har försökt.
Här är lite tips till dig:
- Börja en tråd genom att skriva frågan. Skriv sedan vad du undrar. Efter det kan du antingen infoga en bild med ditt försök till en lösning, eller använda korrekt matematisk notation.
- För att skriva korrekt matematisk notation: använd rotenur-tecknet i menyn (3:e från höger):

Om du trycker på det kommer en ruta att dyka upp där du kan skriva ordentliga bråk, multiplikationstecken etc. Detta underlättar enormt när man ska hjälpa. Om du vill infoga en bild med din lösning kan du trycka på bildikonen (4:e från höger) och följa stegen i rutan som dyker upp.
3. Om du skulle ångra någonting du skrev / hitta ett stavfel, redigera inlägget. På Pluggakuten får man redigera sitt första inlägg under 2 timmar efter att det postades. Detta gör man genom att trycka på redigera längst ner till höger i kanten. Om det är ett inlägg i en tråd som du vill redigera kan du göra det under 1 timme efter att det postades genom att använda samma metod.
Om du följer dessa steg lovar jag dig att du kommer få snabbare och mer effektiv hjälp.
Stort lycka till önskar jag. Du är en riktig kämpe.
Ok, så man använer sig intee av y som man har från början o sätter det lika med.
Och glömde ta med x:et ,hade enbart k.Tror ibland att k och x e lika men dem skiljer sig.
Ok, så det e dem x och y-värdena sm skall användas för att få ut m, testar.
1/a= -(1/a2)*a+m är detta korrekt uppställt?
Ja det är korrekt uppställt.
Vet du hur man kommer vidare?
Jo, jag förstår M,
Jag kan inte använda mig av det/matematisk notation då det handlar primärt om okunskap, det kommer när man lärt sig, dock slarvar jag också ibland där jag kan vara mer tydligt,kanske.
Jag ska ta med mig om att redigera något iställlet för nytt inlägg, bara jag vet hur och vart man gör det.
Jo, tycker på mitt sätt att jag visar visst hur jag försöker o tänker när jag fått stegberäkning,dock inte med infogade bilder.
Det e du/ni som kräver för mycket, med mig får man ha tålamod också, handlar om en balans så jag först lär mig grunderna, det matematiska tänket och nöta in det, det e något som ni måste förstå och som vissa gör andra inte.
Jag infogar inte bilder nej, sant, men skriver i ord istället när jag fått saker förklarade med steg. Så det e en balans att jag försöker och tänker på dessa råd som du,ni ger men att ni också förstår att det handlar om okunskap då blir det förhoppningsvis bättre, det e ett teamwork..:)
Mvh/H
Försöker få in så mycket som möjligt inför NP om några veckor som sagt o som ni säkert förstår, som äldre..:)
Okej. Nu verkar det som vi alla är på samma sida.
Kommer du vidare med uppgiften?
Ledtråd
Lös ut m.
använder sig inte
som
Vart finns redigering?
Hm, nja, man * in a i parentesen men sedan?
Här finns redigering:
Lägg in uttrycket efter att du multiplicerat in a i parentesen.
Vad verkar rimligt att göra enligt balansmetoden?
Ledtråd
Kan man förkorta termen som du multiplicerade a in i på något sätt?
Ser några termer i ekvationen lika ut (har lika nämnare)? Om ja, få dessa ensamma på en sida och m ensamt på en sida.
Visa ditt försök!
Ok, såg det nu, tack.
Missade den helt, men låg ju synligt..:)
Ok, in med a i parentesen, vilka ser lika ut, få dem på samma sida o m ensamt, yes, försöker.
Nja, får det till 1/a= -a/a3 +m korrekt?
Om så hur får jag över det till VL?
Mvh/H
Nej, se över multiplikationen. Jag skrivet ut det du skrivit så får du hitta själv var det blivit knasigt:
Hm, vet inte, men ska man bara * in a med täljaren och inte med nämnaren?
Precis. Bara täljaren.
Efter det kan du förkorta bort a.
Kan du tänka ut det?
Ok, testar.
Hur då får då 1/a= -a/a2 +m?
Hur förkortar jag bort något a här?
ok, så - sitter före ,gällande både täljaren och nämnaren
Prova med att dividera a i både täljare och nämnare i termen med a2.
När man multiplicerar in a är det samma sak som att multiplicera in a/1. Där blir det bara med täljaren (då vid multiplikation av bråk görs täljaren för sig och nämnaren för sig).
så det blir 1/a=- 1/a+ m
1/a+1/a=m?
Vad?
Precis. Väldigt bra.
Addera nu 1/a med 1/a (eftersom de har samma nämnare).
Ok, så ja fick det rätt alltså?
Blir det 2/a=m?
Super. Det blev rätt!
Nu måste du skriva tangentens ekvation i sin helhet eftersom du både har k-värde och m-värdet.
ok, skriver in det
y= -1/a2 +2/a Har jag glömt något?
Kommer knappt ihåg frågan nu..heheh
Bevisa att triangeln har 2 a.e..
arean= b*h/2
Vad görs..
b*h/2
En sak har du glömt, och det är x!
Jag skriver ut ekvationen:
Hur får man fram triangelns bas och höjd (som du behöver för arean)? Kolla på bilden!
Henrik 2 skrev:b*h/2
Glöm inte att redigera inlägget! Annars blir tråden för stökig!
oavsett vart på kurvan som tangenten tangerar kurvan..
Ops, ja,skulle redigerat,glömde av det i alla hast, gamla vanor...
Glömde jag x:et, var det inte ett a istället för x ?
Vad är x då?
Ok, man skriver bara ut x så, man har inte räknat ut det.
Jag ska först läsa igenom tråden för att se hur ni började. Vill inte missleda dig.
Medan jag gör det, kan du fundera på hur man kan skriva koordinaterna för punkterna jag markerat med hjälp av en tangents ekvation.
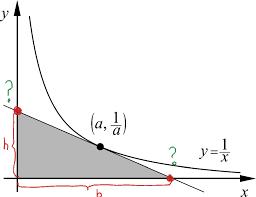
Är y höjden dvs 1/a och basen är x som är a?
Tar en paus nu,tillbaka senare, hade väl en drös andra uppgifter som jag lade ut o tror inte jag fått svar på dem alla.
Mvh/H
Vad jag kan utläsa använde satte ni in a i x för att hitta lutningen vilket stämmer, men a är inte x från och med nu.
Jag tycker att vi sammanfattar vad vi gjort hittills så kanske det blir tydligare vad som bör göras:
- Hitta tangentens lutning. Tangenten har samma lutning som kurvan 1/x i den punkt där de tangerar. Kurvan 1/x har lutningen som är derivatan i den punkten. För hitta lutningen deriverar vi först. Då får vi -1/x2. Eftersom vi är i en punkt där x = a sätter vi in a i det uttrycket och får -1/a2.
- I punkten x = a har tangenten alltså lutningen -1/a2. Nu måste vi hitta tangentens ekvation. Eftersom vi vet en punkt där tangenten skär (a, 1/a) kan vi sätta in det i vår ekvationen för tangenten. Detta ger oss tangentens ekvation:
- Nu måste vi hitta höjden och basen för triangeln. Vi kan se att y-koordinaten för tangentens skärningspunkt med y-axeln = höjden. Vi kan se att x-koordinaten för tangentens skärningspunkten med x-axeln = basen. Skriv ut dessa.
- Med hjälp av basen och höjden från föregående steg, skriv ett uttryck för arean och förenkla: vad får du då?
Ok, då ska man kika på räta linjens ekvation som vi beräknat. y=kx+m
Är m höjden (Y) således 2/a eller är höjden (y)= -1/a 2x+2/a höjden?
Och basen är x som är vad....-1/a2 x ?
Lite svårt..:)
När man fått ut b och h så tar man väl det b*h/2 i en triangel?
Mvh/H
Kolla på min bild som jag infogade. Där finns svaret till dina frågor. Läs punkt nr. 3 igen.
Kommer du vidare?
Ta det lugnt och metodiskt. Skriv ut ekvationen och försök hitta skärningspunkterna.
Ditt uttryck för höjden stämmer. Det är 2/a. Varför? Visa hur du kom fram till det.
För basen stämmer det ej. Du vill lösa ekvationen y = 0.
Ok, det är 2/a för att det är m som då skär y-axeln där?
Nehe, så basen e inte korrekt, får kika o se om jag förstår.
Jag ska alltså lösa en ekvation för att få ut x o sätter den till y=0?
0=-1/a2 x+2/a?
Ja.
"Ditt uttryck för höjden stämmer. Det är 2/a. Varför? Visa hur du kom fram till det." Besvara detta så kan jag hjälpa dig om du inte förstått anledningen bakom!
Förstår inte vad basen x ska vara .Sätter vilken ekvation =0?
Jag såg det då m=2/a och m skär y-axeln. Vill du ha en annan förklaring så vet jag inte då får du förklara
Den förklaringen räcker. Bra tänkt.
Henrik 2 skrev:Förstår inte vad basen x ska vara .Sätter vilken ekvation =0?
Fundera. Hur kan vi få fram skärningspunkten med x-axeln?
Kolla på bilden.
När funktionen skär x-axeln är y = 0, hänger du med på det?
Därför måste du sätta tangentens ekvation till 0 och lösa vid vilket x-värde den blir 0.
y=0 ger
0=-1/a2 x+2/a? Eller ska man använda x istället för a här, hur blir det då?
Mvh/H
Precis. Inget x = a.
Lös ut vad x blir.
Men e denna ekvation korrekt?
0=-1/x2 *x+2/x?
Du menade att man skulle ha a istället för x som jag skrev?
Hej,
Tack men nej , hänger Inte med på vad basen är
Mvh/H
Basen är avståndet från y-axeln till tangentens skärning med x-axeln. Laguna Trinity2 beräknar detta ganska långt ner i inlägg #72. Om man kallar x-koordinaten för b så skall man beräkna när t(b) = 0, d v s
Ok, så basen/b är avståndet mellan x o y-axeln, dess skärning med y-axeln, på/genom den räta linjen?
Men basen brukar väl enbart vara basen och inte det avståndet som går upp till y-axeln, hänger inte med?
Denna uppgift blev så lång o svår så svårt att hänga med nu när jag gör andra tal parallellt.
Så man lägger in b istället för x som beteckning,ok.
2a-b/a2= 0 får jag till 2-b/a=0 är detta korrekt och om så hur får man b fritt o det blir 2a?
Mvh/H
Jag skrev fel, jag har rättat till det nu.
E inte med, men hade lite frågor ovan,i mitt sista inlägg. Denna får man kämpa med för förståelsen.
Titta på Trinity2:s bild i inlägg #72. Där är basen avståndet mellan origo och punkten b, och höjden är avståndet mellan origo och punkten h.
Kikar, men du sade att avståndet på b var den räta linjen, som jag uppfattade, från b upp till där den skär y-axeln?
Ok, ser från origo ut till b, men vad finns i b då, du har sagt det men förstår det inte?
Mvh/H
Läs i mitt inlägg #74, eller i Trinitys #72.
Kikar igen.
Hur får man ut b?
2a-b/a2= 0 får jag till 2-b/a=0 är detta korrekt och om så hur får man b fritt o det blir 2a?
, multiplicera med a2 på båda sidor så blir det 2a-b = 0, addera b på båda sidor så är du klar.
Ok, så istället för att göra som jag försökte med så tar man a2 o multiplicerar det med 0 så blir det 0 kvar i HL,aha. Så har man kvar i VL 2a-b=0 o man flyttar över b så det blir 2a=b
Ok, då har man höjden som e m 2/a och b som e 2a tar man då
2a* 2/a/2 Hur blir den upställningen?
Mvh/H
Blir det * med 1/2 när man flyttar upp 2 från nämnaren?
Försök att låta bli att tänka "flytta". Det ställer ofta till problem.
Tönk istället att du utför samma räkneoperation på bägge sidor av likhetstecknet.
=========
Exempel 1:
x/2 = 3
För att bli av med tvåan i nämnaren så kan du multiplicera bägge sidor med 2:
2*x/2 = 2*3
Förenkla:
x = 6
=========
Exempel 2:
x-3 = 4
För att bli av med trean i vänsterledet så kan du addera 3 till bägge sidor:
x-3+3 = 4+3
Förenkla:
x = 7
=========
Exempel 3:
x+5 = 13
För att bli av med femman i vänsterledet så kan du subtrahera 5 från bägge sidor:
x+5-5 = 13-5
Förenkla:
x = 8
=========
Exempel 4:
4x = 18
För att bli av med fyran i vänsterledet så kan du dividera båda sidor med 4::
4x/4 = 18/4
Förenkla:
x = 4,5
=========
Denna metod för ekvationslösning kallas balansmetoden.
Jag menar balansering och inte flytta, fel ord bara
Men se min undring över uppställning för att lösa uppgiften.
Mvh/H
Du frågar om du ska multiplicera med 1/2 för att bli av med en 2a i nämnaren?
Ja, se inlägg 72 där T gör så får att få ut arean, e inte riktigt med. O även mitt inlägg 85.
/H
Henrik 2 skrev:[...]
Ok, då har man höjden som e m 2/a och b som e 2a tar man då
2a* 2/a/2 Hur blir den upställningen?
Om höjden är .och basen är så får vi att arean blir
Precis så jag ställde upp det, men visste inte hur man gör med ett sådant tal.
Ok, så man multiplicerar 2a med täljaren (2an) enbart , o får 4a i täljaren och a i nämnaren ovanför bråket och dessa a tar ut varandra och sedan 4/2=2.
Ingen aningen om det tillvägagångssättet.
Mvh/H
Har väl mer eller mindre förstått uppgiften men kan någon förtydliga i inlägg 72 från T med bild. Står tangenten i punkten P ges av:....................................
Förstod inte allt som ingick o där man kommer fram till 2a-b/a2 som man sedan använder sig av för att få ut b.
Mvh/H
Henrik 2 skrev:[...]
Ok, så man multiplicerar 2a med täljaren (2an) enbart , o får 4a i täljaren och a i nämnaren ovanför bråket och dessa a tar ut varandra och sedan 4/2=2.
Ingen aningen om det tillvägagångssättet.
Du kan börja med att skriva som bråket .
Då blir täljaren
När du multiplicerar ihop dessa bråktal så får du , vilket är lika med .
Om detta känns ovant så bör du nog repetera den del av algebran som handlar om bråktal.
E med på att 2a= 2a/1 och då blir nämnaren 1,ok. Bara svårt har inte beräknat sådana tal, men förstår.
Kan du kika inlägg 93 då jag inte förstår inlägg 72 under punkten där det står tangenten i punkten P ges av:....................................
Förstod inte allt som ingick o där man kommer fram till 2a-b/a2 som man sedan använder sig av för att få ut b.
Henrik 2 skrev:Kan du kika inlägg 93 då jag inte förstår inlägg 72 under punkten där det står tangenten i punkten P ges av:....................................
Trinity2 använder sig av något som kallas enpunktsformeln. Slå upp den i din bok eller googla. Den är väldigt praktisk att använda ibland.
Men det går även att göra på andra sätt.
Jag kan visa ett annat sätt här:
Tangenten är en rät linje, villet innebär att den kan skrivas på formen , där är linjens lutning och är y-koordinaten för den punkt där linjen skär y-axeln.
Vi vet sedan tidigare att linjens lutning i tangeringspunkten är .
Det betyder att tangentens ekvation kan skrivas .
Vi vill nu ta reda på vad har för värde.
Då kan vi använda att sambandet gäller för alla punkter som ligger på linjen.
Vi vet att tangeringspunkten ligger på linjen.
Denna punkt har x-koordinaten och y-koordinaten .
Eftersom sambandet ska gälla för den punkten så kan sätta in istället för och istället för I linjens ekvation och den ska fortfarande gälla.
Om vi gör det så får vi
Vi förenklar högerledet genom att multiplicera ihop med och vi får då
Vi förenklar högerledet igen genom att förkorta första termen med och vi får då
Om vi nu använder balansmetoden och adderar till båda sidor så får vi
Efter förenkling får vi
Vi har nu kommit fram till att tangentens ekvation är
=========
Nu vill vi ta reda på triangelns bas och höjd.
Basen är lika med avståndet mellan y-axeln och den punkt där tangenten skär x-axeln.
Tangenten skär x-axeln där y = 0.
Det ger oss ekvationen
Vi använder balansmetoden och adderar till båda sidor.
Vi får då
Efter förenkling får vi
Vi använder balansmetoden och multiplicerar båda sidor med :
Efter förenkling får vi
Det betyder att triangelns bas
Nu vill vi ta reda på triangelns höjd.
Höjden är lika med avståndet mellan x-axeln och den punkt där tangenten skär y-axeln. Denna vet vi redan eftersom det är lika med linjens m-värde.
Triangelns höjd är alltså
Hängde du med på allt nu?
Ok, förstår lite mer nu, förstod inte enpunktsformeln. Bara b som jag inte förstod hur man fick ut ,just nu..:)
b lika med avståndet från/mellan y-axeln och den punkt där tangenten skär x-axeln, yes. Här e y=0 o då sätter man tangentens ekvation = 0 för att få ut basen(x)
balanserar "flyttar",heheh, från HL till VL och får 1/a2 x=2/a .
Därefter * båda sidor med a2 för att få bort nämnaren i VL,ok.
Sedan får man stryka a2 o X blir kvar i VL o i HL kvar a*2 som blir 2a
Sedan byter man ut x mot b som då blir 2a. yes e med nu på denna förklaring.
så 2a*2/a/2
4a/a/2
4/2=2 a.e
Härligt
Mvh/H