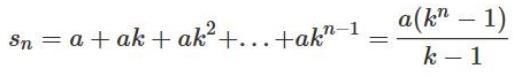Ma3 annuitetslån
Hej!
Jag försöker lösa en uppgift som lyder såhär:
"Amir ska köpa en bil för 209 515 kronor och ansöker därför om ett banklån. Amir har
hittat ett erbjudande om ett annuitetslån där han får välja hur stort belopp han vill
betala varje år, inkl. årsränta på 9,5% och amortering. Sedan gör banken en beräkning
på hur många år han behöver göra inbetalningar. Amir räknar ut att han klarar av att
betala 30 000 kronor per år, med start ett år efter det att lånet tagits. Hur lång tid tar
det att betala av lånet?"
Jag tänker man använda sig av denna formel:
Där a= 30 000 och K= 1,095. Men sedan fastnar jag. Hur ska jag ta mig vidare och tänker jag rätt?
Du vet även att Sn=209 515. Sätt in det också och lös ut n.
Jag har försökt med det men får inget svar. Därför tänkte jag att S är slutvärdet och 209 515 är inte slutvärdet på lånet utan nyvärdet.
Smaragdalena skrev:Du vet även att Sn=209 515. Sätt in det också och lös ut n.
Jag har försökt med det men får inget svar. Därför tänkte jag att S är slutvärdet och 209 515 är inte slutvärdet på lånet utan nyvärdet.
Oj, det har du ju rätt i. Man måste ju betala räntan också.
Då kan man gå den hårda vägen och räkna år för år. Första året lånar han 209 515. Räntan blir 19 904 kr, och han betalar 30 000 kr. Det nya värdet på lånet blir alltså 209 515.1,095-30 000 = 199 419 kr.
Nästa år är lånet på 199 419 kr, räntan blir 18 945 kr och det nya beloppet blir 188 364 kr. Sedan blir det 176 259kr det fjärde året och 163 000 det femte. Sedan vill nog Amir köpa en ny bil. Då har han betalat 150 000 kr och skulden har minskat med 46 500 kr ungefär.
Smaragdalena skrev:Oj, det har du ju rätt i. Man måste ju betala räntan också.
Då kan man gå den hårda vägen och räkna år för år. Första året lånar han 209 515. Räntan blir 19 904 kr, och han betalar 30 000 kr. Det nya värdet på lånet blir alltså 209 515.1,095-30 000 = 199 419 kr.
Ja, man skulle kunna räkna år för år men tror det måste finnas ett smartare sätt :/
Uppgiften avser ett annuitetslån, vilket innebär att summan av avbetalningen och räntan på lånet är årligen konstant, i detta fall endast 30 000kr.
Tillämpbar formel hittar man t.ex. här:
Man kan ju börja ställa upp beräkningarna med bokstäver i stället för siffror och se om man hittar ett mönster:
B = bilens pris, r = räntesatsen, A = amortering annuitet L= lånets storlek.
- L1=B(1+r)-A)
- L2=(B(1+r)-A)(1+r)-A
- L3=((B(1+r)-A)(1+r)-A)(1+r)-A
- L4=(((B(1+r)-A)(1+r)-A)(1+r)-A)(1+r)-A eller L=B(1+r)4-A(1+r)3-A(1+r)2-A(1+r)
Här tycker jag att det börjar synas ett mönster!
Summan kan man skriva om till ett bekvämare uttryck, och så skall Ln vara 0 när hela bilen äntligen är betald. Sedan borde det gå att lösa ut n.
EDIT: Du har rätt Affe! Tack.
Smaragdalena skrev:Man kan ju börja ställa upp beräkningarna med bokstäver i stället för siffror och se om man hittar ett mönster:
B = bilens pris, r = räntesatsen, A = amortering L= lånets storlek.
- L1=B(1+r)-A)
- L2=(B(1+r)-A)(1+r)-A
- L3=((B(1+r)-A)(1+r)-A)(1+r)-A
- L4=(((B(1+r)-A)(1+r)-A)(1+r)-A)(1+r)-A eller L=B(1+r)4-A(1+r)3-A(1+r)2-A(1+r)
Här tycker jag att det börjar synas ett mönster!
Summan kan man skriva om till ett bekvämare uttryck, och så skall Ln vara 0 när hela bilen äntligen är betald. Sedan borde det gå att lösa ut n.
Amorteringsbeloppet (A) är inte konstant, men du kan väl kalla det för annuitet (A).
Tillämpbar formel hittar man t.ex. här:
https://sv.wikipedia.org/wiki/Annuitetslån
Efter att ha bearbetat ovanstående får jag:
Vilket ger n=12år
Smaragdalena skrev:Man kan ju börja ställa upp beräkningarna med bokstäver i stället för siffror och se om man hittar ett mönster:
B = bilens pris, r = räntesatsen, A = amortering annuitet L= lånets storlek.
- L1=B(1+r)-A)
- L2=(B(1+r)-A)(1+r)-A
- L3=((B(1+r)-A)(1+r)-A)(1+r)-A
- L4=(((B(1+r)-A)(1+r)-A)(1+r)-A)(1+r)-A eller L=B(1+r)4-A(1+r)3-A(1+r)2-A(1+r)
Här tycker jag att det börjar synas ett mönster!
Summan kan man skriva om till ett bekvämare uttryck, och så skall Ln vara 0 när hela bilen äntligen är betald. Sedan borde det gå att lösa ut n.
EDIT: Du har rätt Affe! Tack.
Hej, även jag har problem med denna uppgift. Du skriver att summan kan skrivas om till ett bekvämare uttryck, men jag förstår inte riktigt hur. Såhär långt har jag kommit fram till följande:
Förstår bara inte riktigt vad som ska stå istället för summan och i detta fallet frågetecknet.
bibliotek10 skrev:Smaragdalena skrev:Man kan ju börja ställa upp beräkningarna med bokstäver i stället för siffror och se om man hittar ett mönster:
B = bilens pris, r = räntesatsen, A = amortering annuitet L= lånets storlek.
- L1=B(1+r)-A)
- L2=(B(1+r)-A)(1+r)-A
- L3=((B(1+r)-A)(1+r)-A)(1+r)-A
- L4=(((B(1+r)-A)(1+r)-A)(1+r)-A)(1+r)-A eller L=B(1+r)4-A(1+r)3-A(1+r)2-A(1+r)
Här tycker jag att det börjar synas ett mönster!
Summan kan man skriva om till ett bekvämare uttryck, och så skall Ln vara 0 när hela bilen äntligen är betald. Sedan borde det gå att lösa ut n.
EDIT: Du har rätt Affe! Tack.
Hej, även jag har problem med denna uppgift. Du skriver att summan kan skrivas om till ett bekvämare uttryck, men jag förstår inte riktigt hur. Såhär långt har jag kommit fram till följande:
Förstår bara inte riktigt vad som ska stå istället för summan och i detta fallet frågetecknet.
Uttrycket med summatecknet kallas för geometrisk summa....
Affe Jkpg skrev:bibliotek10 skrev:Smaragdalena skrev:Man kan ju börja ställa upp beräkningarna med bokstäver i stället för siffror och se om man hittar ett mönster:
B = bilens pris, r = räntesatsen, A = amortering annuitet L= lånets storlek.
- L1=B(1+r)-A)
- L2=(B(1+r)-A)(1+r)-A
- L3=((B(1+r)-A)(1+r)-A)(1+r)-A
- L4=(((B(1+r)-A)(1+r)-A)(1+r)-A)(1+r)-A eller L=B(1+r)4-A(1+r)3-A(1+r)2-A(1+r)
Här tycker jag att det börjar synas ett mönster!
Summan kan man skriva om till ett bekvämare uttryck, och så skall Ln vara 0 när hela bilen äntligen är betald. Sedan borde det gå att lösa ut n.
EDIT: Du har rätt Affe! Tack.
Hej, även jag har problem med denna uppgift. Du skriver att summan kan skrivas om till ett bekvämare uttryck, men jag förstår inte riktigt hur. Såhär långt har jag kommit fram till följande:
Förstår bara inte riktigt vad som ska stå istället för summan och i detta fallet frågetecknet.
Uttrycket med summatecknet kallas för geometrisk summa....
Aha! Hur ska den geometriska summan skrivas? Formeln är ju , men vad ska jag stoppa in istället för a och k?
Jämför Smaragdalenas summa med
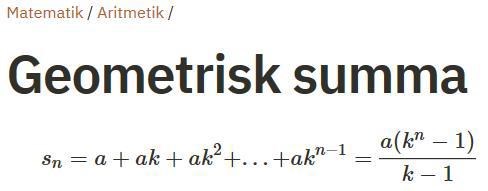
Affe Jkpg skrev:Tillämpbar formel hittar man t.ex. här:
https://sv.wikipedia.org/wiki/Annuitetslån
Efter att ha bearbetat ovanstående får jag:
Vilket ger n=12år
Affe Jkpg skrev:Jämför Smaragdalenas summa med
Stämmer det?
bibliotek10 skrev:Affe Jkpg skrev:Jämför Smaragdalenas summa med
Stämmer det?
Nä, Smaragdalenas summa börjar inte på k=0. Justera för det.
Börjar jag närma mig nu?
Lösning nummer 1: Jag har redan presenterat en lösning för dig.
Lösning nummer 2: Nu är du inne på lösning nummer två, som tycks vara en långt större utmaning för dig än lösning nummer 1. Du är långt ifrån att närma dig en lösning. Du ska inte alls sätta in några värden på variablerna, utan hålla dig till bokstavsekvationer ett tag till.
vilket du jämför med: