Maclaurinpolynom av 8.grad

Geometrisk serie.

$\frac{1}{1-q}=\sum _{k=0}^{\infty }{q}^k$, |q| < 1.

Hej!

Utan att veta vad övning 1.87 är så är det lite svårt. Om jag får gissa är det möjligtvis någonting med att $1+x+x^2+x^3+...=\dfrac{1}{1-x}$ om $\vert x\vert <1$.

I så fall kan du skriva att $\dfrac{1}{1+x^3}=\dfrac{1}{1-\left(-x^3\right)}=1-x^3+x^6-...$ (om $\vert -x^3\vert<1$). 

Ett alternativ är att inse att:

$f(x)=\frac{d}{dx}(\frac{1}{3}\cdot \ln(1+x^3))$

tackar.

Jag har inte förstått hur jag kan lösa det utan att derivara 8 gånger :( 

Har kollat på många videor men hittade inte något som förklarar lättare om maclaurinpolynom och substition . De flesta av dem berättar på universitet nivå, tycker jag. Men jag vet inte om det är så 

Jag studerar matematik spealisering. Det är kanske inte så detaljerad som man lär sig på universitetet. 

Men jag har svårt att förstå det. Jag kan formeln och enkla frågor som att hitta andra graden , 4. graden... men när det gäller substition för högre grad, kan jag inte för jag inte förstått. Imorgon har jag provet. Ska bli väldigt tacksam om någon förklarar,löser uppgiften på ett enklare sätt, om ni har tid. 

Skulle bli väldigt tacksam också om ni rekomenderar  någon länk från youtube eller hemsida som förklarar och ger exempel på Maclaurinserie på min nivå. 

Tack på förhand.

Är du med på att du kan skriva (för rimliga $x$) att $f\left(x\right)=x^2\cdot\left(1-x^3+x^6-x^9+x^{12}-...\right)=?$ där du själv får förenkla och ersätta frågetecknet. 

Sen är det bara att beräkna derivatorna av denna oändliga summa (du kan derivera termvis) i punkten $a=0$ för att hitta Maclaurinpolynomet. Du kommer att märka att många av dessa är lika med noll. 

Men i slutändan, ja, du behöver derivera $8$ gånger och se vad du får, men eftersom det är polynom är det enkelt och många av derivatorna är dessutom lika med noll som sagt.

Moffen skrev:

Är du med på att du kan skriva (för rimliga $x$) att $f\left(x\right)=x^2\cdot\left(1-x^3+x^6-x^9+x^{12}-...\right)=?$ där du själv får förenkla och ersätta frågetecknet. 

Sen är det bara att beräkna derivatorna av denna oändliga summa (du kan derivera termvis) i punkten $a=0$ för att hitta Maclaurinpolynomet. Du kommer att märka att många av dessa är lika med noll. 

Men i slutändan, ja, du behöver derivera $8$ gånger och se vad du får, men eftersom det är polynom är det enkelt och många av derivatorna är dessutom lika med noll som sagt.

Tack så mycket.  Ja, jag har förstått den delen. X^2 * ( 1-×^3+×^6...) 

Men vet inte vad jag bör göra efter det.  när jag beräknar derivatorna av summar, blir alla 0. :( 

så svaret blir 0 enligt mig :D men i facit något helt annat :D 

Då räknar du fel, och det är svårt att veta vad för fel du gör om du inte visar oss.

Efter förenkling får du alltså $f\left(x\right)=x^2-x^5+x^8-x^{11}+x^{14}-...$. Så $f\left(0\right)=f'\left(0\right)=0$, men $f''\left(0\right)=2$. Så där har du exempelvis en nollskild term. 

Elif Sidar skrev:

Moffen skrev:

Är du med på att du kan skriva (för rimliga $x$) att $f\left(x\right)=x^2\cdot\left(1-x^3+x^6-x^9+x^{12}-...\right)=?$ där du själv får förenkla och ersätta frågetecknet. 

Sen är det bara att beräkna derivatorna av denna oändliga summa (du kan derivera termvis) i punkten $a=0$ för att hitta Maclaurinpolynomet. Du kommer att märka att många av dessa är lika med noll. 

Men i slutändan, ja, du behöver derivera $8$ gånger och se vad du får, men eftersom det är polynom är det enkelt och många av derivatorna är dessutom lika med noll som sagt.

Tack så mycket.  Ja, jag har förstått den delen. X^2 * ( 1-×^3+×^6...) 

Men vet inte vad jag bör göra efter det.  när jag beräknar derivatorna av summar, blir alla 0. :( 

så svaret blir 0 enligt mig :D men i facit något helt annat :D 

f(0)=0 eftersom att alla termer inneåller x, samma sak med 1:a derivatan, men vid 2:a derivatan så får vi ju vår första konstant från den första termen (x^2) som bara blir 2 och alla andra termer blir 0. Vid tredje derivatan så blir allt 0 igen och så fortsätter det så här. Exponenterna ökar ju med 3, så efter var tredje derivata så får vi en konstant när vi stoppar in x=0. Så om vi deriverar 8 gånger så borde vi få totalt 3 tal, dvs 2, -5! och 8!

MathematicsDEF skrev:

Elif Sidar skrev:

Visa föregående citat

Moffen skrev:

Är du med på att du kan skriva (för rimliga $x$) att $f\left(x\right)=x^2\cdot\left(1-x^3+x^6-x^9+x^{12}-...\right)=?$ där du själv får förenkla och ersätta frågetecknet. 

Sen är det bara att beräkna derivatorna av denna oändliga summa (du kan derivera termvis) i punkten $a=0$ för att hitta Maclaurinpolynomet. Du kommer att märka att många av dessa är lika med noll. 

Men i slutändan, ja, du behöver derivera $8$ gånger och se vad du får, men eftersom det är polynom är det enkelt och många av derivatorna är dessutom lika med noll som sagt.

Tack så mycket.  Ja, jag har förstått den delen. X^2 * ( 1-×^3+×^6...) 

Men vet inte vad jag bör göra efter det.  när jag beräknar derivatorna av summar, blir alla 0. :( 

så svaret blir 0 enligt mig :D men i facit något helt annat :D 

f(0)=0 eftersom att alla termer inneåller x, samma sak med 1:a derivatan, men vid 2:a derivatan så får vi ju vår första konstant från den första termen (x^2) som bara blir 2 och alla andra termer blir 0. Vid tredje derivatan så blir allt 0 igen och så fortsätter det så här. Exponenterna ökar ju med 3, så efter var tredje derivata så får vi en konstant när vi stoppar in x=0. Så om vi deriverar 8 gånger så borde vi få totalt 3 tal, dvs 2, -5! och 8!

Så efter att vi har hittat alla derivator gör vi så här eller hur; 

f(0)+f'(0)*× f'(0) *×^2/2! ....

Det som vi gjorde från början (substition) var för att glra enklare beräkningar av derivator. Med detta hittar vi derivator sedan multiplicerar vi dem med X ^n och dividersr med n! 

Eller hur 🙈🙈🙈

Elif Sidar skrev:

MathematicsDEF skrev:

Visa föregående citat

Elif Sidar skrev:

Moffen skrev:

Är du med på att du kan skriva (för rimliga $x$) att $f\left(x\right)=x^2\cdot\left(1-x^3+x^6-x^9+x^{12}-...\right)=?$ där du själv får förenkla och ersätta frågetecknet. 

Sen är det bara att beräkna derivatorna av denna oändliga summa (du kan derivera termvis) i punkten $a=0$ för att hitta Maclaurinpolynomet. Du kommer att märka att många av dessa är lika med noll. 

Men i slutändan, ja, du behöver derivera $8$ gånger och se vad du får, men eftersom det är polynom är det enkelt och många av derivatorna är dessutom lika med noll som sagt.

Tack så mycket.  Ja, jag har förstått den delen. X^2 * ( 1-×^3+×^6...) 

Men vet inte vad jag bör göra efter det.  när jag beräknar derivatorna av summar, blir alla 0. :( 

så svaret blir 0 enligt mig :D men i facit något helt annat :D 

f(0)=0 eftersom att alla termer inneåller x, samma sak med 1:a derivatan, men vid 2:a derivatan så får vi ju vår första konstant från den första termen (x^2) som bara blir 2 och alla andra termer blir 0. Vid tredje derivatan så blir allt 0 igen och så fortsätter det så här. Exponenterna ökar ju med 3, så efter var tredje derivata så får vi en konstant när vi stoppar in x=0. Så om vi deriverar 8 gånger så borde vi få totalt 3 tal, dvs 2, -5! och 8!

Så efter att vi har hittat alla derivator gör vi så här eller hur; 

f(0)+f'(0)*× f'(0) *×^2/2! ....

 

Det som vi gjorde från början (substition) var för att glra enklare beräkningar av derivator. Med detta hittar vi derivator sedan multiplicerar vi dem med X ^n och dividersr med n! 

 

Eller hur 🙈🙈🙈

Precis, vi har vårt f(x) och nu är det bara att skriva ner det polynom som vi får av Maclauren, dvs: 

$\sum _{n=0}^{\infty }\frac{f^n\left(0\right)}{n!}{x}^n$, fast vi tar bara med de första 8 termerna då det är av grad 8 som efterfrågas (de flesta termerna blir ju 0 ändå).

MathematicsDEF skrev:

Elif Sidar skrev:

Visa föregående citat

Moffen skrev:

Är du med på att du kan skriva (för rimliga $x$) att $f\left(x\right)=x^2\cdot\left(1-x^3+x^6-x^9+x^{12}-...\right)=?$ där du själv får förenkla och ersätta frågetecknet. 

Sen är det bara att beräkna derivatorna av denna oändliga summa (du kan derivera termvis) i punkten $a=0$ för att hitta Maclaurinpolynomet. Du kommer att märka att många av dessa är lika med noll. 

Men i slutändan, ja, du behöver derivera $8$ gånger och se vad du får, men eftersom det är polynom är det enkelt och många av derivatorna är dessutom lika med noll som sagt.

Tack så mycket.  Ja, jag har förstått den delen. X^2 * ( 1-×^3+×^6...) 

Men vet inte vad jag bör göra efter det.  när jag beräknar derivatorna av summar, blir alla 0. :( 

så svaret blir 0 enligt mig :D men i facit något helt annat :D 

f(0)=0 eftersom att alla termer inneåller x, samma sak med 1:a derivatan, men vid 2:a derivatan så får vi ju vår första konstant från den första termen (x^2) som bara blir 2 och alla andra termer blir 0. Vid tredje derivatan så blir allt 0 igen och så fortsätter det så här. Exponenterna ökar ju med 3, så efter var tredje derivata så får vi en konstant när vi stoppar in x=0. Så om vi deriverar 8 gånger så borde vi få totalt 3 tal, dvs 2, -5! och 8!

Hur får du formellt sett tag på 1:a derivatan? Det är ju en oändlig summa du har och inte en ändlig summa.

Det är lite farligt att derivera i summan då vi egentligen byter plats på två gränsvärden (derivata-gränsvärde och oändlig summa-gränsvärdet). Ska man göra det måste man ha en motivation för det. Isåfall bör man kolla t.ex. likformig konvergens eller något annat argument för varför det är ok först.

MathematicsDEF skrev:

Elif Sidar skrev:

Visa föregående citat

MathematicsDEF skrev:

Elif Sidar skrev:

Visa föregående citat

Moffen skrev:

Är du med på att du kan skriva (för rimliga $x$) att $f\left(x\right)=x^2\cdot\left(1-x^3+x^6-x^9+x^{12}-...\right)=?$ där du själv får förenkla och ersätta frågetecknet. 

Sen är det bara att beräkna derivatorna av denna oändliga summa (du kan derivera termvis) i punkten $a=0$ för att hitta Maclaurinpolynomet. Du kommer att märka att många av dessa är lika med noll. 

Men i slutändan, ja, du behöver derivera $8$ gånger och se vad du får, men eftersom det är polynom är det enkelt och många av derivatorna är dessutom lika med noll som sagt.

Tack så mycket.  Ja, jag har förstått den delen. X^2 * ( 1-×^3+×^6...) 

Men vet inte vad jag bör göra efter det.  när jag beräknar derivatorna av summar, blir alla 0. :( 

så svaret blir 0 enligt mig :D men i facit något helt annat :D 

f(0)=0 eftersom att alla termer inneåller x, samma sak med 1:a derivatan, men vid 2:a derivatan så får vi ju vår första konstant från den första termen (x^2) som bara blir 2 och alla andra termer blir 0. Vid tredje derivatan så blir allt 0 igen och så fortsätter det så här. Exponenterna ökar ju med 3, så efter var tredje derivata så får vi en konstant när vi stoppar in x=0. Så om vi deriverar 8 gånger så borde vi få totalt 3 tal, dvs 2, -5! och 8!

Så efter att vi har hittat alla derivator gör vi så här eller hur; 

f(0)+f'(0)*× f'(0) *×^2/2! ....

 

Det som vi gjorde från början (substition) var för att glra enklare beräkningar av derivator. Med detta hittar vi derivator sedan multiplicerar vi dem med X ^n och dividersr med n! 

 

Eller hur 🙈🙈🙈

Precis, vi har vårt f(x) och nu är det bara att skriva ner det polynom som vi får av Maclauren, dvs: 

$\sum _{n=0}^{\infty }\frac{f^n\left(0\right)}{n!}{x}^n$, fast vi tar bara med de första 8 termerna då det är av grad 8 som efterfrågas (de flesta termerna blir ju 0 ändå).

Tack så mycket 

JohanB skrev:

MathematicsDEF skrev:

Visa föregående citat

Elif Sidar skrev:

Moffen skrev:

Är du med på att du kan skriva (för rimliga $x$) att $f\left(x\right)=x^2\cdot\left(1-x^3+x^6-x^9+x^{12}-...\right)=?$ där du själv får förenkla och ersätta frågetecknet. 

Sen är det bara att beräkna derivatorna av denna oändliga summa (du kan derivera termvis) i punkten $a=0$ för att hitta Maclaurinpolynomet. Du kommer att märka att många av dessa är lika med noll. 

Men i slutändan, ja, du behöver derivera $8$ gånger och se vad du får, men eftersom det är polynom är det enkelt och många av derivatorna är dessutom lika med noll som sagt.

Tack så mycket.  Ja, jag har förstått den delen. X^2 * ( 1-×^3+×^6...) 

Men vet inte vad jag bör göra efter det.  när jag beräknar derivatorna av summar, blir alla 0. :( 

så svaret blir 0 enligt mig :D men i facit något helt annat :D 

f(0)=0 eftersom att alla termer inneåller x, samma sak med 1:a derivatan, men vid 2:a derivatan så får vi ju vår första konstant från den första termen (x^2) som bara blir 2 och alla andra termer blir 0. Vid tredje derivatan så blir allt 0 igen och så fortsätter det så här. Exponenterna ökar ju med 3, så efter var tredje derivata så får vi en konstant när vi stoppar in x=0. Så om vi deriverar 8 gånger så borde vi få totalt 3 tal, dvs 2, -5! och 8!

Hur får du formellt sett tag på 1:a derivatan? Det är ju en oändlig summa du har och inte en ändlig summa.

Det är lite farligt att derivera i summan då vi egentligen byter plats på två gränsvärden (derivata-gränsvärde och oändlig summa-gränsvärdet). Ska man göra det måste man ha en motivation för det. Isåfall bör man kolla t.ex. likformig konvergens eller något annat argument för varför det är ok först.

Tack så mycket 

Moffen skrev:

Då räknar du fel, och det är svårt att veta vad för fel du gör om du inte visar oss.

Efter förenkling får du alltså $f\left(x\right)=x^2-x^5+x^8-x^{11}+x^{14}-...$. Så $f\left(0\right)=f'\left(0\right)=0$, men $f''\left(0\right)=2$. Så där har du exempelvis en nollskild term. 

Tack så mycket 

tomast80 skrev:

Ett alternativ är att inse att:

$f(x)=\frac{d}{dx}(\frac{1}{3}\cdot \ln(1+x^3))$

Tack så mycket 

PATENTERAMERA skrev:

Geometrisk serie.

$\frac{1}{1-q}=\sum _{k=0}^{\infty }{q}^k$, |q| < 1.

Tack så mycket

JohanB skrev:

MathematicsDEF skrev:

Visa föregående citat

Elif Sidar skrev:

Moffen skrev:

Är du med på att du kan skriva (för rimliga $x$) att $f\left(x\right)=x^2\cdot\left(1-x^3+x^6-x^9+x^{12}-...\right)=?$ där du själv får förenkla och ersätta frågetecknet. 

Sen är det bara att beräkna derivatorna av denna oändliga summa (du kan derivera termvis) i punkten $a=0$ för att hitta Maclaurinpolynomet. Du kommer att märka att många av dessa är lika med noll. 

Men i slutändan, ja, du behöver derivera $8$ gånger och se vad du får, men eftersom det är polynom är det enkelt och många av derivatorna är dessutom lika med noll som sagt.

Tack så mycket.  Ja, jag har förstått den delen. X^2 * ( 1-×^3+×^6...) 

Men vet inte vad jag bör göra efter det.  när jag beräknar derivatorna av summar, blir alla 0. :( 

så svaret blir 0 enligt mig :D men i facit något helt annat :D 

f(0)=0 eftersom att alla termer inneåller x, samma sak med 1:a derivatan, men vid 2:a derivatan så får vi ju vår första konstant från den första termen (x^2) som bara blir 2 och alla andra termer blir 0. Vid tredje derivatan så blir allt 0 igen och så fortsätter det så här. Exponenterna ökar ju med 3, så efter var tredje derivata så får vi en konstant när vi stoppar in x=0. Så om vi deriverar 8 gånger så borde vi få totalt 3 tal, dvs 2, -5! och 8!

Hur får du formellt sett tag på 1:a derivatan? Det är ju en oändlig summa du har och inte en ändlig summa.

Det är lite farligt att derivera i summan då vi egentligen byter plats på två gränsvärden (derivata-gränsvärde och oändlig summa-gränsvärdet). Ska man göra det måste man ha en motivation för det. Isåfall bör man kolla t.ex. likformig konvergens eller något annat argument för varför det är ok först.

Vi vet hur f(x) ser ut och vi förstår dess mönster, det är ett väldigt enkelt polynom som bara innehåller koefficienter, x samt heltalsexponenter. Samt derivatan av en summa är summan av derivatorna, så man deriverar bara varje term för sig. När vi deriverar denna oändliga summa första gången så är det bara att följa mönstret och då vet vi exakt hur varje term ända till n:te termen ser ut. Vi vet att $f\left(x\right)=x^2-x^5+x^8-x^{11}+...$, och därav blir $f\text{'}\left(x\right)=2x-5x^4+8x^7-11x^{10}+14x^{13}+...$, exponenterna ökar för alltid så därför är vi säkra på att vi inte får någon konstant just här, och när vi stoppar in x=0 så blir allt 0 eftersom att alla termer innehåller x. Men vid just andraderivatan så får vi vår första konstant, alltså derivatan av 2x som bara är 2, vilket inte är beroende av x alls, så när vi stoppar in x=0 så får vi bara 2 och allt annat är 0, så fortsätter det just så här var tredje derivata.

Se en lösning nedan:

Jag tycker att det är många och smarta lösningsförslag som har diskuterats i tråden hittills, men någonstans kan jag tycka att ni krånglar till det lite genom att blanda in serier. Inte för att jag har något emot serier, men de är lite meckiga att jobba med om man vill vara helt stringent. Framför allt är det inte alls uppenbart att man kan derivera en potensserie term för term inom konvergensradien, utan det är något som kräver ett ordentligt bevis (se t.ex. den här blogposten av självaste Timothy Gowers), och jag vet inte om TS har kommit dit ännu. 

Nu var det länge sedan jag lärde mig om Maclaurinutvecklingar, så jag kanske förbiser något, men ungefär så här hade jag tänkt om jag fick den här uppgiften.

Det finns två sätt att definiera Maclaruinpolynomet av grad 8 för en funktion $f(x)$ som är deriverbar minst 8 gånger i punkten $x=0$. Det ena är med hjälp av en formel:

Definition 1. Maclaurinpolynomet av grad 8 ges av formeln

   $\displaystyle P_8{(x)}={f(0) + f'(0)x} + \frac{f''(0)}{2!}x^2 + \cdots + \frac{f^{(8)}(0)}{8!}x^8\,.$

I princip skulle du nu kunna derivera din funktion 8 gånger med hjälp av kvotregeln och de andra deriveringsreglerna, evaluera vid $x=0$ och sedan räkna fram svaret. Det skulle vara massa jobb, men det fungerar, och om du har tillgång till en dator som kan hålla koll på alla termer i derivatorna är det fullt görbart. Du kan t.ex. fråga Wolfram Alpha vad $f^{(8)}(0)$ är så här!

Den andra definitionen ger igen explicit formel, utan tar i stället fasta på vilka egenskaper Maclaurinpolynomet har:

Definition 2. Macluarinpolynmet av grad 8 är det unika polynom $P_8(x)$ med gradtal max 8, som har egenskapen att

   $\,{f(x)} = {P_8(x)} + \underbrace{{\color{blue}B(x)}x^9}_\mathrm{felterm}$

för någon funktion $B(x)$ som är begränsad (dvs. sticker inte iväg mot oändligheten) för $x\approx 0$.

Annorludna uttryckt: $f(x)=P_8(x) + \mathcal{O}(x^9)$.

Att det verkligen finns ett unikt sådant polynom $P_8(x)$ och att det är precis det polynom som anges i Definition 1 är lite smått magiskt, och visas antagligen som en sats i din mattebok.

Jag är personligen ett stort fan av Definition 2, eftersom den gör det möjligt att bygga ihop Macluarinutvecklingar för komplicerade funktioner, med hjälp av kända Maclaurinutvecklarn för enklare funktioner!

I ditt fall kan vi börja med funktionen $\frac{1}{1-t}$. Du har säkert Maclaurinutvecklat den femtielva gånger redan, annars kan du säkert för hand verifiera att vi har följande andragradsutveckling (du kommer se senare varför det räcker med grad 2):

   $\displaystyle\frac{1}{1-t}=1+t+t^2+\underbrace{B(t)t^3}_\mathrm{felterm}$,  där $B(t)$ är begränsat för $t\approx 0$.

Bra! Nu kan kan vi bygga på den här funktionen till en funktion som liknar $f(x)$ lite mer, genom att ersätta $t$ med $-x^3$. Då får vi

  $\displaystyle\frac{1}{1+x^3}=\frac{1}{1-(-x^3)}={1+(-x^3)+(-x^3)^2}+{B(-x^3)(-x^3)^3}=1-x^3+x^6-\underbrace{B(-x^3)x^9}_\mathrm{felterm}\,.$

Och sen behöver vi bara multiplicera in $x^2$ för att få $f(x)$, så här:

   $\displaystyle {f(x)}=x^2\cdot \frac{1}{1+x^3}={x^2(1-x^3+x^6-B(-x^3)x^9)}=x^2-x^5+x^8\,\underbrace{{\color{blue}-\,{B(-x^3)}x^2} x^{9}}_\mathrm{felterm}\,.$

Voilà: en åttagradsapproximation av $f(x)$.

Det enda vi behöver göra nu är att kontrollera så att feltermen matchar formen i Definition 2. Och visst gör den det. Om $B(t)$ är begränsat för $t\approx 0$, så kommer $-B(-x^3)$ vara begränsat för $x\approx 0$. För $x\approx 0$ kommer dessutom $x^2$ att vara pyttelitet, så $-B(-x^3)x^2$ kommer också att vara begränsat. Så ja, vi har tydligen hittat Maclaurinpolynomet av grad 8.

Slutsats: $P_8(x)=x^2-x^5+x^8$.

Notera: Om vi bakar ihop $x^2$ och $x^9$ i feltermen, så ser vi att feltermen faktiskt har gradtal 11, så vårt polynom är även lika med $P_9(x)$ och $P_{10}(x)$.

Följdfråga: Kan du upprepa argumentet ovan för att bestämma ett Maclaurinpolynom av högre grad, t.ex. $P_{11}(x)$? Hur lång utveckling av $\frac{1}{1-t}$ måste du starta med för att den slutgiltiga utvecklingen av $f(x)$ ska få tillräckligt högt gradtal på feltermen?

Jag har en fråga om definitionerna här.

Om vi tex har f(x) = P₈(x) + H(x)x⁹, där H är heavisidefunktionen, så är väl f inte ens deriverbar i 0, och kan väl då inte sägas ha ett Maclaurinpolynom av ordningen 8, eftersom Maclaurinutvecklingen kräver deriverbarhet. Eller?

Måste vi inte säga något i stil med: om f är nio gånger kontinuerligt deriverbar i 0 och om vi kan skriva f(x) enligt f(x) = P₈(x) + O(x⁹), där P₈(x) är något polynom av grad mindre eller lika med 8,  så måste P₈(x) vara lika Maclaurinpolynomet av ordningen 8?

Hm, jag håller med om att premissen i mitt förra inlägg nog blev lite för svag (det behöv nog en extra derivata, och dessutom behöver nog deriverbarhet i en omgivning runt origo). Dessutom blev Definition 2 lite otydligt (det räcker att approximationen gäller i närheten av origo).

Jag tror satsen jag har i åtanke är något i stil med följande, men jag får nog återigen reservera mig för att jag kanske missar något viktigt:

Sats. Låt $f(x)$ vara en funktion som är $n+1$ gånger kontinuerligt deriverbar på ett öppet intervall runt $x=0$. Då existerar det ett unikt polynom $P_n(x)$ med gradtal max $n$ med följande egenskap:

Det existerar en öppen omgivning av $x=0$ där $f(x)$ kan skrivas på formen $f(x)=P_n(x)+B(x)x^{n+1}$ för en begränsad funktion $B(x)$. 

Detta unika polynom ges av formeln

   $\displaystyle {P_n(x)}=\sum_{k=0}^n\frac{f^{(k)(0)}}{k!}x^k$

och kallas för Maclaurinpolyomet av grad $n$ för funktionen $f$.

Vi skulle då fortsatt kunna tänka oss att vi har två ekvivalenta definitioner: antingen använder vi formeln som definition, eller så använder vi den kursiverade egenskapen hos Maclaurinpolynom som definition.

Låter dettaa rätt, eller har någon av forumets alla klippska analysmännsikor något mer motexempel i bakfickan? 😉

ogghi, vad händer om man tillämpar din definition av Maclaurinutveckling på följande funktion?

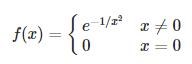
tomast80 skrev:

ogghi, vad händer om man tillämpar din definition av Maclaurinutveckling på följande funktion?

Vi får prova helt enkelt!

Låt oss till att börja med fixera att positivt heltal $n$; eftersom funktionen är oändligt deriverbar på hela $\mathbb{R}$, så kommer premissen i satsen att vara uppfylld oavsett vilket $n$ vi väljer.

Vidare är det ganska enkelt att övertyga sig med hjälp av derivatans definition om att

   $f'(0)=f''(0)=\cdots=f^{(n)}(0)=0\,,$

så om vi använder formeln för det $n$:te maclaurinpolynomet i mitt förra inlägg så får vi $P_n(x)=0$, dvs. det konstanta nollpolynomet. Intressant!

Kvar att kontrollera är nu huruvida detta verkligen är en tillräckligt bra approximation av $f(x)$ i närheten av $x=0$ för att den kursiverade egenskapen i mitt förra inlägg ska vara uppfylld. Och det är den så vitt jag kan se! Vi kan nämligen skriva

   $\displaystyle {f(x)}=0+\underbrace{{\color{blue}\frac{e^{-1/x^2}}{x^{n+1}}}x^{n+1}}_\mathrm{felterm}\,,$

där det är relativt enkelt att övertyga sig om att den blåmarkerade biten är begränsad nära $x=0$; t.ex. så kan vi notera att

   $\displaystyle\lim_{x\to 0} \frac{e^{-1/x^2}}{x^{n+1}}=\lim_{t\to\pm\infty}\frac{t^{n+1}}{e^{t^2}}=0\,.$

Med andra ord så är $f(x)=0+\mathcal{O}(x^{n+1})$, så jag tror att allt är frid och fröjd! ^_^

(Men det finns många små subtila fallgropar i analys, så jag kanske missar något.)

Det här makear för övrigt väldigt mycket sense rent visuellt också: funktionen är väldigt lik den konstanta funktionen $0$ i närheten av $x=0$, vilket följande figur visar: