Maclaurinutveckla invers funktion

Är inversen till sin2x+ln(1+4x), arcsin2x+e^(1+4x)? Eller vad annars?
Nej, hur kom du fram till det? Det finns ingen sluten form för inversen.
Du får använda något samband mellan derivatorna av funktionen och dess invers.
Edit: det kanske räcker med att veta McLaurin-utvecklingen av funktionen oxh sedan ansätta ett polynom av rätt grad.
Hej,
Utvecklingen du söker är
Inversa funktionssatsen talar om hur derivatorna ska beräknas.
Albiki skrev:Hej,
Utvecklingen du söker är
Inversa funktionssatsen talar om hur derivatorna ska beräknas.
Vad är inversa funktionssatsen?
tomast80 skrev:Lite bra tips här: https://math.stackexchange.com/questions/249253/second-derivative-of-the-inverse-function
Förstår du hur de gör? Skulle du kunna förklara lite
Sätt
Enligt länken gäller sedan att:
Inversa funktionssatsen: https://sv.wikipedia.org/wiki/Inversa_funktionssatsen
tomast80 skrev:Sätt
Enligt länken gäller sedan att:
Fick det här, varför blir det fel?
Några fel ovan. Börjar med förstaderivatan:
tomast80 skrev:Några fel ovan. Börjar med förstaderivatan:
får då andraderivatan: -2/9, vilket fortfarande blir fel
Varför blir andraderivatan ?
Dualitetsförhållandet skrev:Varför blir andraderivatan ?
Har du kollat härledningen i länken? Om du påstår att det är formeln till höger, hur har du då härlett/fått fram den?
När jag gör som jag funderade på ovan så får jag först f(x) = 6x - 8x2 + o(x3). Med ansatsen f-1(y) = a + bx + cx2 får jag sedan f-1(y) = y/6 + y2/27 + o(y3).
Jag brukar lösa sånna här med samma metod som laguna. Men ansatsen blir onödigt lång här.
Visa spoiler
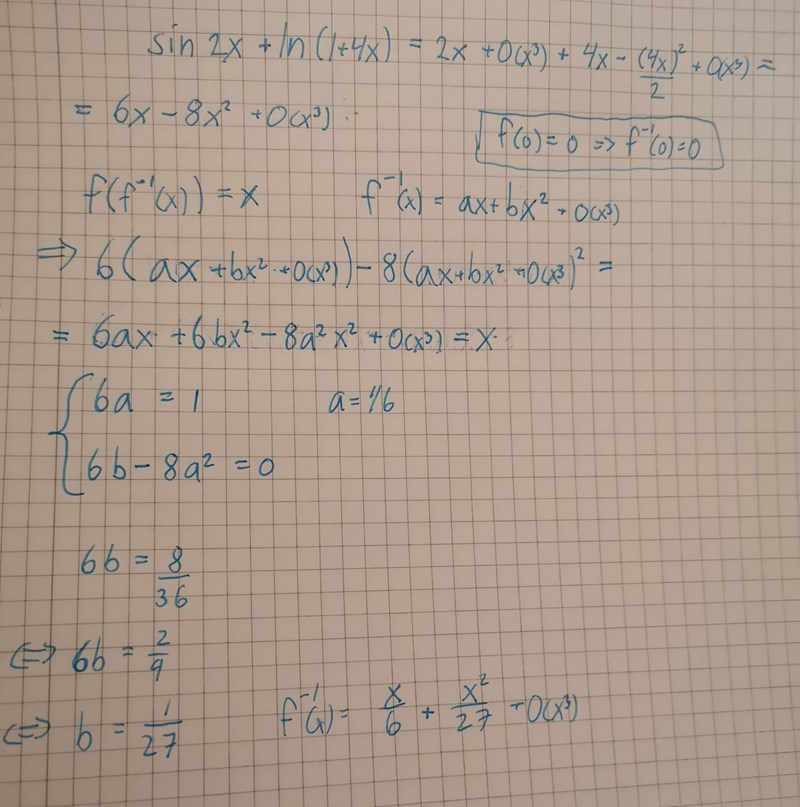
Hej,
Först bestäms värdet via sambandet till att vara .
Därefter ger Inversa funktionssatsen derivatan
Inversens andraderivata ges av Kedjeregeln.
Med och blir den sökta andraderivatan




