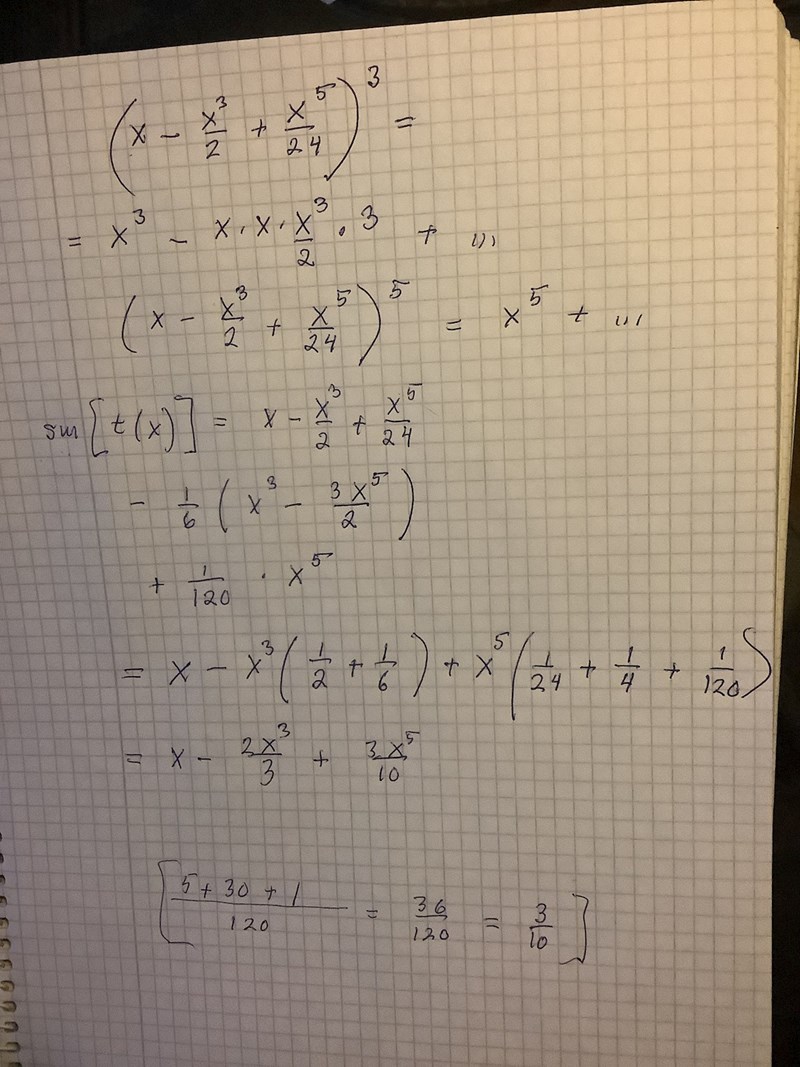Maclaurinutveckla sin(xcos(x))
Jag har fastnar på en uppgift där jag ska bestämma maclaurinpolynomet av grad 5 till f(x). Min lösning ser ut som följande, men blir helt fel:
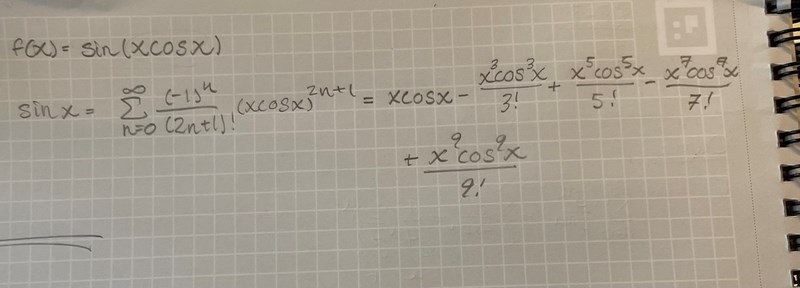
Jag tycker att ett svar i cos x när man ska utveckla sinus inte ger så mycket.
Så jag skulle börja med x cosx = x – x3/2! + x5/4! = t(x)
Därefter skulle jag utveckla sin [t(x)] = t – t3/3! + t5/5!
Det ser jobbigt ut men du behöver ju bara bry dig om de x-termer som får grad ≤ 5.
Mogens skrev:Jag tycker att ett svar i cos x när man ska utveckla sinus inte ger så mycket.
Så jag skulle börja med x cosx = x – x3/2! + x5/4! = t(x)
Därefter skulle jag utveckla sin [t(x)] = t – t3/3! + t5/5!
Det ser jobbigt ut men du behöver ju bara bry dig om de x-termer som får grad ≤ 5.
Hmmm... kör fast när jag ska förenkla sin[t(x)]
Ett sätt är att derivera funktionen så man får f'(0), f''(0) osv. Om det är ett bra sätt här vet jag inte.
Kanske inte här, men absolut ett sätt att ha i verktygslådan!
Där du skriver för bökigt, tänk på att graden alltid blir högre än 5 när du gångrar ihop x5 med något annat, så det är lika bra att stryka den och utveckla med pascals triangel/binomialsatsen.
Knepet är som Micimako påpekar att inte utveckla parenteser i onödan och genast avfärda i alla termer över ett visst gradtal. Samtidigt ska man ha med "tillräckligt" många termer för att det ska bli tydligt vad man gör.
Vi börjar med att notera två serieutvecklingar
Vårt sökta uttryck kommer därmed bestå av
Nu studerar vi varje term för sig och sätter in uttrycket för utvecklingen av . Den första termen ger
Den andra termen ger
Den sista termen ger bara ett enda bidrag med tillräckligt låg potens, nämligen
Om vi nu åter lägger ihop termerna ser vi alltså att
D4NIEL skrev:Knepet är som Micimako påpekar att inte utveckla parenteser i onödan och genast avfärda i alla termer över ett visst gradtal. Samtidigt ska man ha med "tillräckligt" många termer för att det ska bli tydligt vad man gör.
Vi börjar med att notera två serieutvecklingar
Vårt sökta uttryck kommer därmed bestå av
Nu studerar vi varje term för sig och sätter in uttrycket för utvecklingen av . Den första termen ger
Den andra termen ger
Den sista termen ger bara ett enda bidrag med tillräckligt låg potens, nämligen
Om vi nu åter lägger ihop termerna ser vi alltså att
Grymt tack till alla svar! Stämmer denna lösningen? Tänker framför allt angående motiveringen vid tredje termen:
Utom att ordon kommer och går ser det ganska bra ut. Vet inte hur petig din lärare är. Men när du tar bort x5 från term 2 måste du ju ändra till x5 i ordo också. Det är precis därför vi har den där, för att berätta att härifrån stryker jag allt.