Maclaurinutveckling
Hej,
Jag har fastnat på följande uppgift:

Jag plockar ut exponentialfunktionen, cosx och sinx för att approximera dessa. Sätter sedan in approximationen i originalekvationen där man då, förhoppningsvis, ska kunna stryka lite termer och sedan bryta ut dominerande term för att se vad som händer då x->0. Dock lyckas jag inte med detta, utan fastnar här:
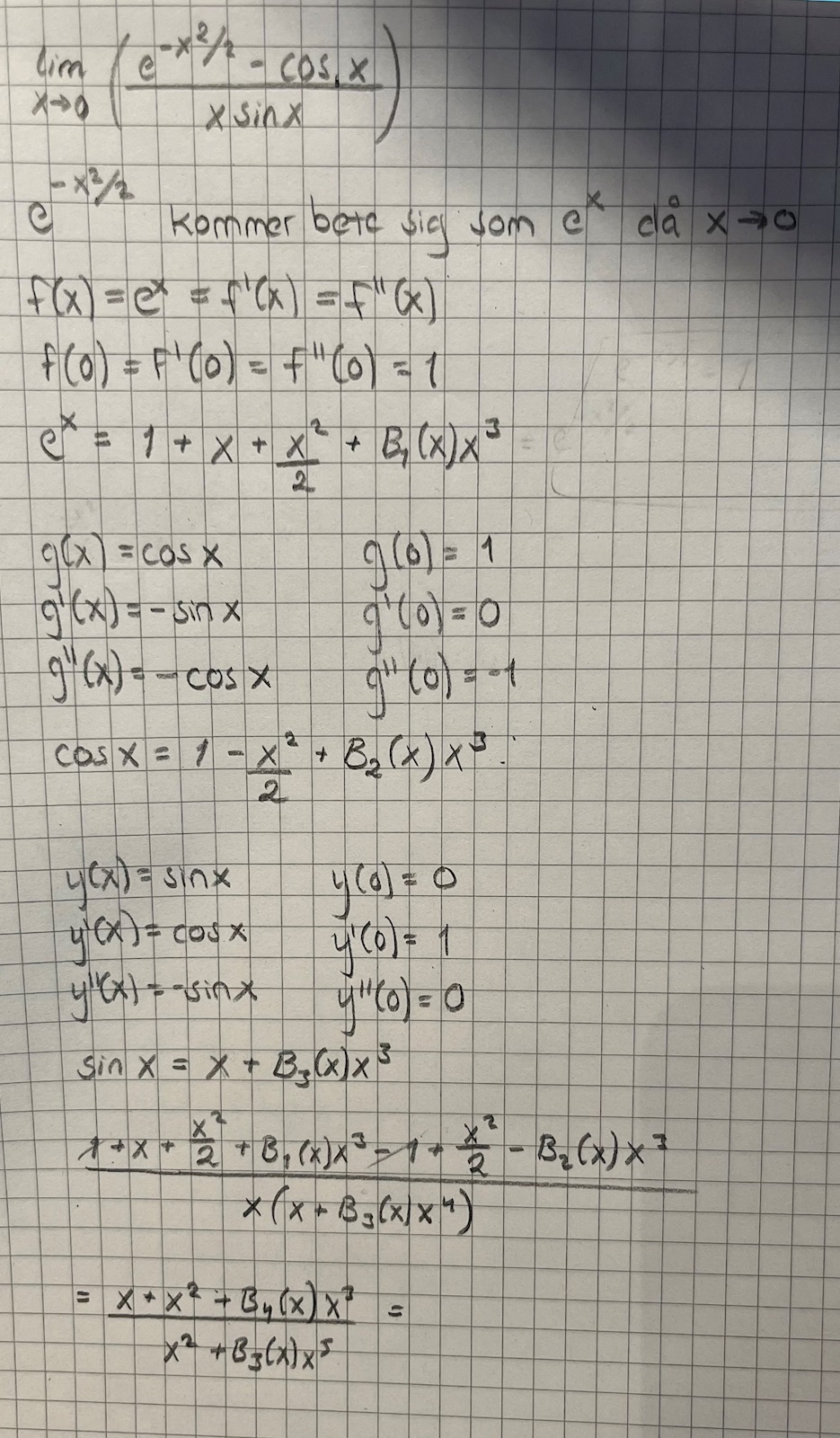
Kan någon se var det går fel, och hur jag borde tänka?
Fel på rad 2.
Varifrån kommer antagandet om att e(...) beter sig som eX för små x?
Prova att inte utveckla sin-fknen utan bara täljaren och sedan utnyttja typen a/sin a —->1 när a—>0.
Dr. G skrev:Fel på rad 2.
Varifrån kommer antagandet om att e(...) beter sig som eX för små x?
Jag bara tänkte att båda kommer närma sig =1 då x->0. Är det ett fel antagande alltså?
Tomten skrev:Prova att inte utveckla sin-fknen utan bara täljaren och sedan utnyttja typen a/sin a —->1 när a—>0.
Kommer det fungera även fast det nu står x * sin x?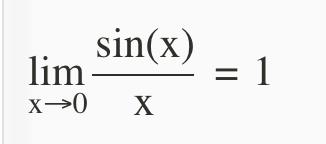
starboy skrev:Dr. G skrev:Fel på rad 2.
Varifrån kommer antagandet om att e(...) beter sig som eX för små x?
Jag bara tänkte att båda kommer närma sig =1 då x->0. Är det ett fel antagande alltså?
Ja, båda går mot 1, men derivatorna är helt olika.
Sätt t = -x2/2
så kan du använda den kända utvecklingen
et = 1 + t + t2/2 + ...
och sedan byta t mot -x2/2.


