MAFY 2007 uppgift 29
Uppgift 29. Hur bestämmer man en sid längd av en romb? Försökte med Pythagoras men jag fick fel

"UPPGIFT" i rubriken ändrat till "uppgift". /Smutstvätt, moderator
Visa ditt försök.
Louis skrev:
Visa ditt försök.
Jag är inte med på hur du tänker där. Du har ritat två olika rätvinkliga trianglar med diagonalernas längder som hypotenusor.
Men romben består av fyra kongruenta rätvinkliga trianglar där halva diagonallängderna är kateter.
Louis skrev:Jag är inte med på hur du tänker där. Du har ritat två olika rätvinkliga trianglar med diagonalernas längder som hypotenusor.
Men romben består av fyra kongruenta rätvinkliga trianglar där halva diagonallängderna är kateter.
Är det en kvadrat eller hur menar du?
Nej, i en kvadrat är diagonalerna lika långa.
Rita en romb, dra diagonalerna (så ser du att romben delas i fyra kongruenta trianglar) och skriv in vad du vet.
Sedan blir det Pythagoras en gång.
En ganska enkel metod som illustrerar Louis poäng är följande:
Rita rombens diagonaler, och rita in romben i en rektangel, där rombens hörn ligger på mitten av rektangelns sidor:
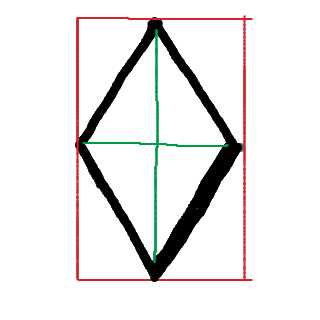
Ser du var Pythagoras kommer in? :)
Louis skrev:
Nej, i en kvadrat är diagonalerna lika långa.
Rita en romb, dra diagonalerna (så ser du att romben delas i fyra kongruenta trianglar) och skriv in vad du vet.
Sedan blir det Pythagoras en gång.
La du inte ut en annan figur nyss? Där de givna längderna satt rätt på diagonalerna. Nu har du satt dem som sidlängder (och då är det inte en romb eftersom sidorna är olika långa). Halva diagonalerna bildar rätvinkliga trianglar (det är något man ska känna till om en romb, att diagonalerna skär varandra under rät vinkel). Där rombens sökta sidlängd är hypotenusa.
Louis skrev:La du inte ut en annan figur nyss? Där de givna längderna satt rätt på diagonalerna. Nu har du satt dem som sidlängder (och då är det inte en romb eftersom sidorna är olika långa). Halva diagonalerna bildar rätvinkliga trianglar (det är något man ska känna till om en romb, att diagonalerna skär varandra under rät vinkel). Där rombens sökta sidlängd är hypotenusa.
Såhär? 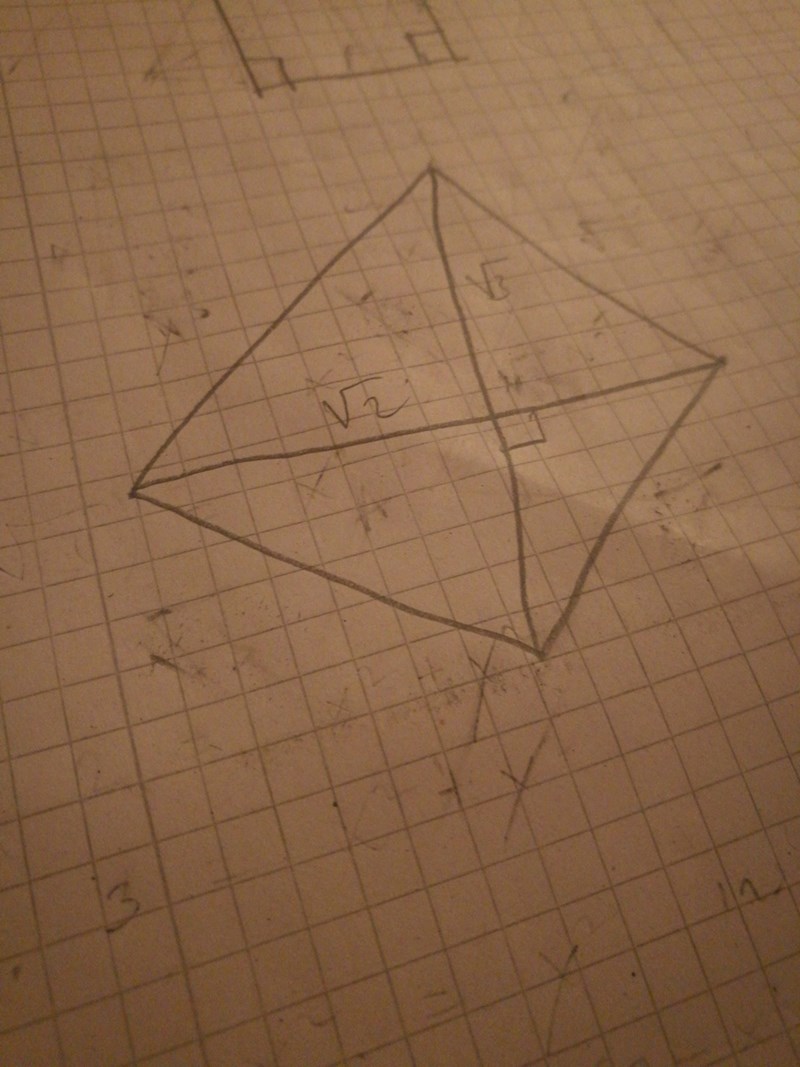
Ja, fast tänk på att och är längderna på hela diagonalerna.
Kateterna i den triangel du tänker använda är hälften av de måtten.
Använd nu Pythagoras sats för att beräkna hypotenusan, dvs rombens sida.
Louis skrev:Ja, fast tänk på att och är längderna på hela diagonalerna.
Kateterna i den triangel du tänker använda är hälften av de måtten.
Använd nu Pythagoras sats för att beräkna hypotenusan, dvs rombens sida.
Pythagoras sats var då? 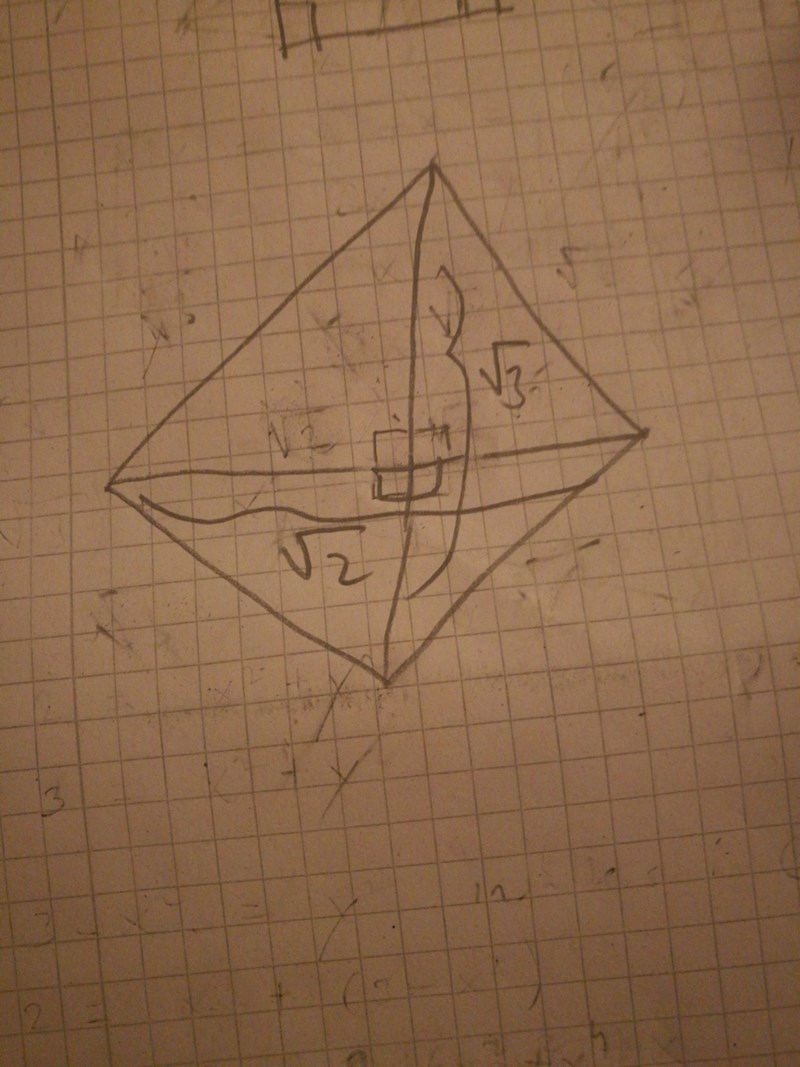
Jovisst, men det hade varit tydligare för uppställningen av ekvationen om du i din förra figur lagt till /2 vid de båda rötterna.
Du har båda kateterna i en rätvinklig triangel och kan använda Pythagoras sats för att beräkna hypotenusan.
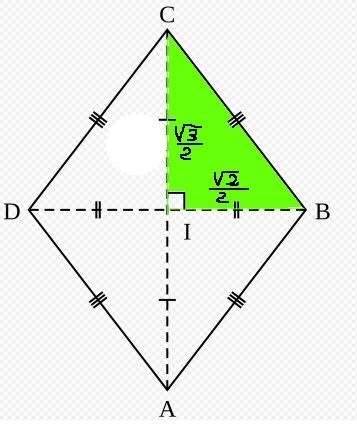
![]()
Louis skrev:Jovisst, men det hade varit tydligare för uppställningen av ekvationen om du i din förra figur lagt till /2 vid de båda rötterna.
Du har båda katerna i en rätvinklig triangel och kan använda Pythagoras sats för att beräkna hypotenusan.
Tack!!


